A body of mass 5 kg moving alonga straight line is accelerated from 4ms−1 to 8ms−1 with the application of a froce of 10 N in the same direction. Then
Work done by the fores is 120 J
Displacement of the body is 12m
Time for the change in velocity is 2s
All the above
The correct Answer is:D
To solve the problem step by step, we will follow the outlined process to find the displacement, work done, and time taken for the body.
Step 1: Calculate the acceleration
We know the force applied and the mass of the body. We can use Newton's second law to find the acceleration.
Force=mass×acceleration
Given:
- Force (F) = 10 N
- Mass (m) = 5 kg
Using the formula:
a=Fm=10N5kg=2m/s2
Step 2: Calculate the displacement using the kinematic equation
We can use the kinematic equation that relates initial velocity, final velocity, acceleration, and displacement:
v2=u2+2as
Where:
- v = final velocity = 8 m/s
- u = initial velocity = 4 m/s
- a = acceleration = 2 m/s²
- s = displacement (what we need to find)
Substituting the values into the equation:
82=42+2⋅2⋅s
Calculating:
64=16+4s
Rearranging to solve for s:
64−16=4s
48=4s
s=484=12m
Step 3: Calculate the work done
Work done (W) is given by the formula:
W=Force×Displacement
Substituting the values:
W=10N×12m=120J
Step 4: Calculate the time taken for the change in velocity
We can use the first equation of motion to find the time taken:
v=u+at
Rearranging to solve for t:
t=v−ua
Substituting the values:
t=8m/s−4m/s2m/s2=42=2s
Summary of Results
- Displacement s=12m
- Work done W=120J
- Time taken t=2s
We know the force applied and the mass of the body. We can use Newton's second law to find the acceleration.
- Force (F) = 10 N
- Mass (m) = 5 kg
We can use the kinematic equation that relates initial velocity, final velocity, acceleration, and displacement:
- v = final velocity = 8 m/s
- u = initial velocity = 4 m/s
- a = acceleration = 2 m/s²
- s = displacement (what we need to find)
48=4s
s=484=12m
Work done (W) is given by the formula:
We can use the first equation of motion to find the time taken:
- Displacement s=12m
- Work done W=120J
- Time taken t=2s
Similar Questions
A body of mass 6 kg is acted on a by a force so that its velocity changes from 3ms−1 to 5ms−1, then change in momentum is
View SolutionA constant force acting on a body of mass 3kg changes its speed from 2ms−1 to 3.5ms−1 in 25 s. The direction of motion of the body remains unchanged. Calculate magnitude and direction of the force.
View Solution
Knowledge Check
A box with a mass of 2kg accelerates in a straight line from 4 m/s to 8m/s due to the application of a force whose duration is 0.5 s. find the average strength of this force.
A2NB4NC8ND16NA constant force acting on a body of mass of 5 kg change its speed from 5ms−1to10ms−1 in 10 s without changing the direction of motion. The force acting on the body is
A1.5NB2NC2.5ND5N
If the velocity v of particle moving along a straight line decreases linearly with its displacement s from 20ms−1 to a value approaching zero at s = 30 m, then acceleration of the particle at v=10ms^(-1) is
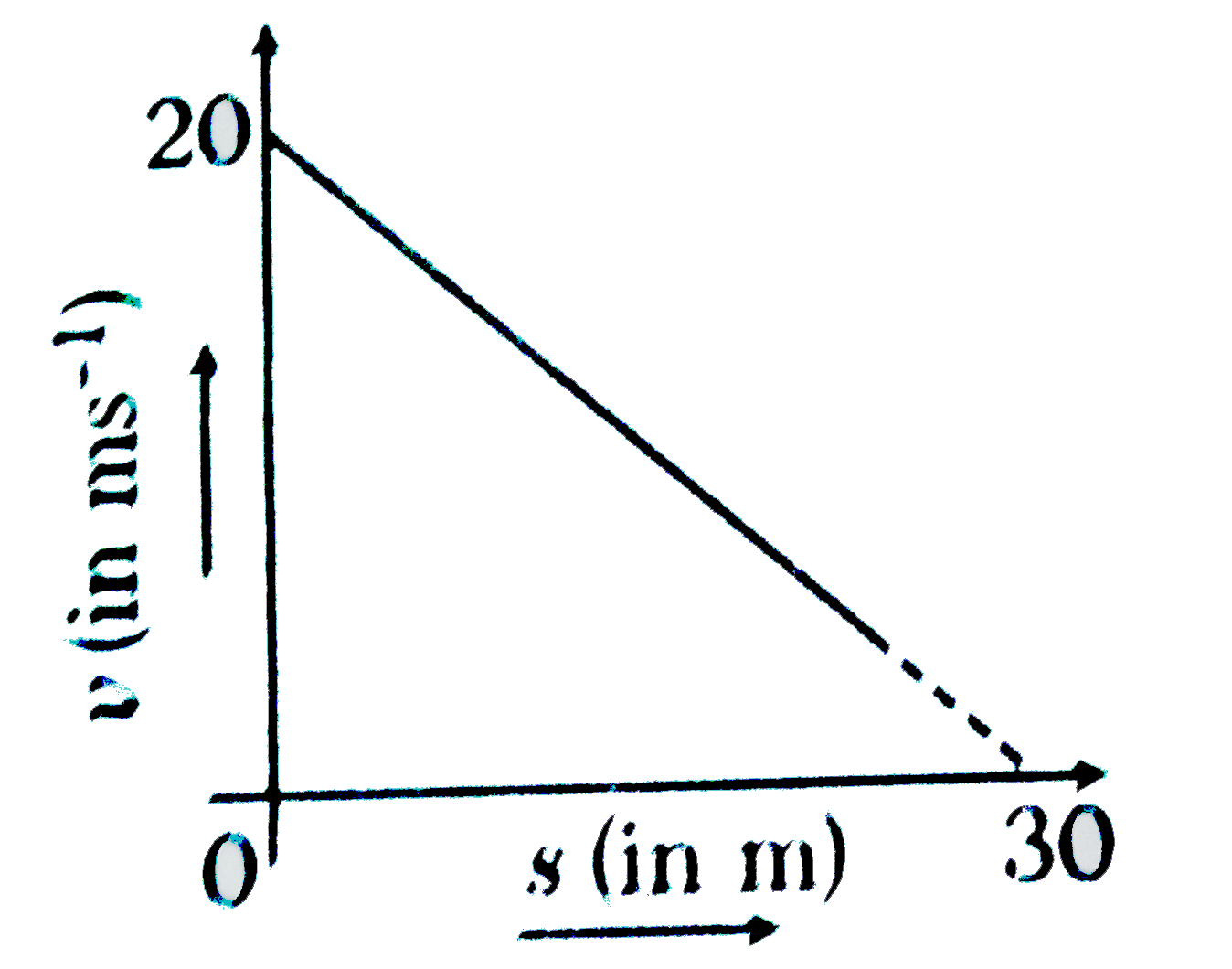
View SolutionA particle moves in a straight line with a constant acceleration. It changes its velocity from 10ms−1 to 20ms−1 while passing through a distance 135m in t seconds. The value of t is.
(a) 10 (b) 1.8 (c) 12 (d) 9
View SolutionAt time t=0, a car moving along a straight line has a velocity of 16ms−1. It slows down with an acceleration of −0.5tms−2, where t is in second. Mark the correct statement (s).
View SolutionDue to the application of a force on a body of mass 100 kg that is initially at rest, the body moves with an acceleration of 20ms−2 in the direction of the force. Find the magnitude of the force.
View SolutionA body of mass 10 kg is moving on a horizonal surface be applying a force of 10 N in the forward direction. The body moves with a constant velocity of 0.2ms−1. Work done by the force of friction in the first 10 seconds is
View SolutionA body of mass 10 kg moving with speed of 3ms−1 collides with another stationary body of mass 5 kg As a result, the two bodies stick togethre. The KE of composite mass will be
View Solution

