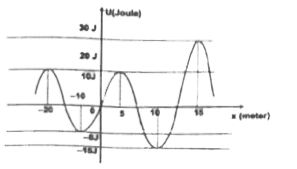
Figure shows the variation of potential energy of a particle as a function of x, the x-coordinate of the region. It has been assumed that potential energy depends only on x. For all other values of x, U is zero, i.e., x←10 and x>15, U=0.
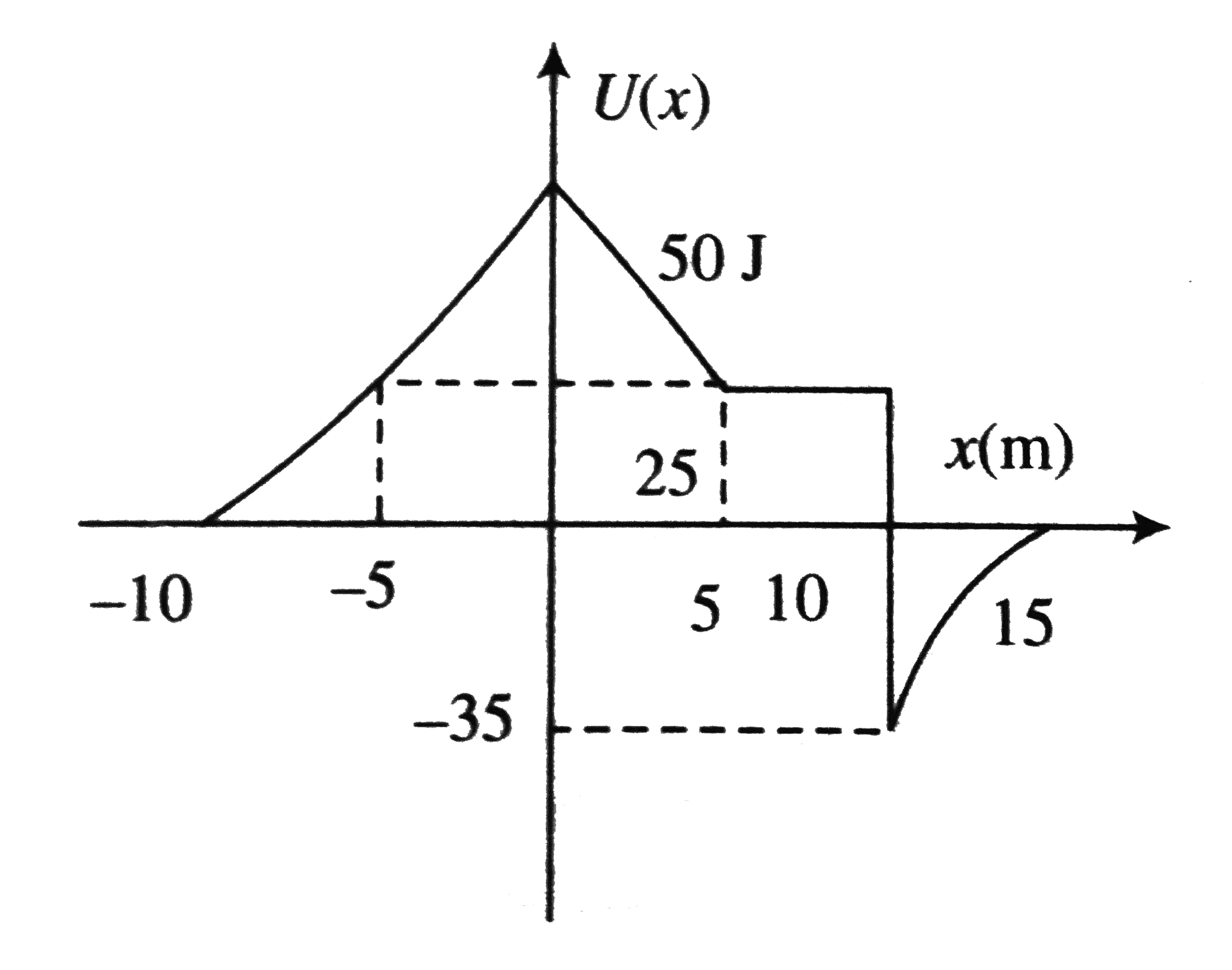
If the particle is isolated and its total mechanical energy is 60J, then
the particle can be found anywhere from −∞<x<∞
the particle's maximum KE is 95 J
the particle 's KE is not getting zero anywhere onX-axis
all of the above are true
The correct Answer is:D
Step by step video solution for Figure shows the variation of potential energy of a particle as a function of x, the x-coordinate of the region. It has been assumed that potential energy depends only on x. For all other values of x, U is zero, i.e., xlarr10 and xgt15, U=0. If the particle is isolated and its total mechanical energy is 60J, then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
The figure shows the variation of potential energy of a particle as a funcation of x, the x-coordinate of the region. It has been assumed that potential energy depends only on x. For all other values x,U is zero. i.e. forx<−10 and x>15,U=0.
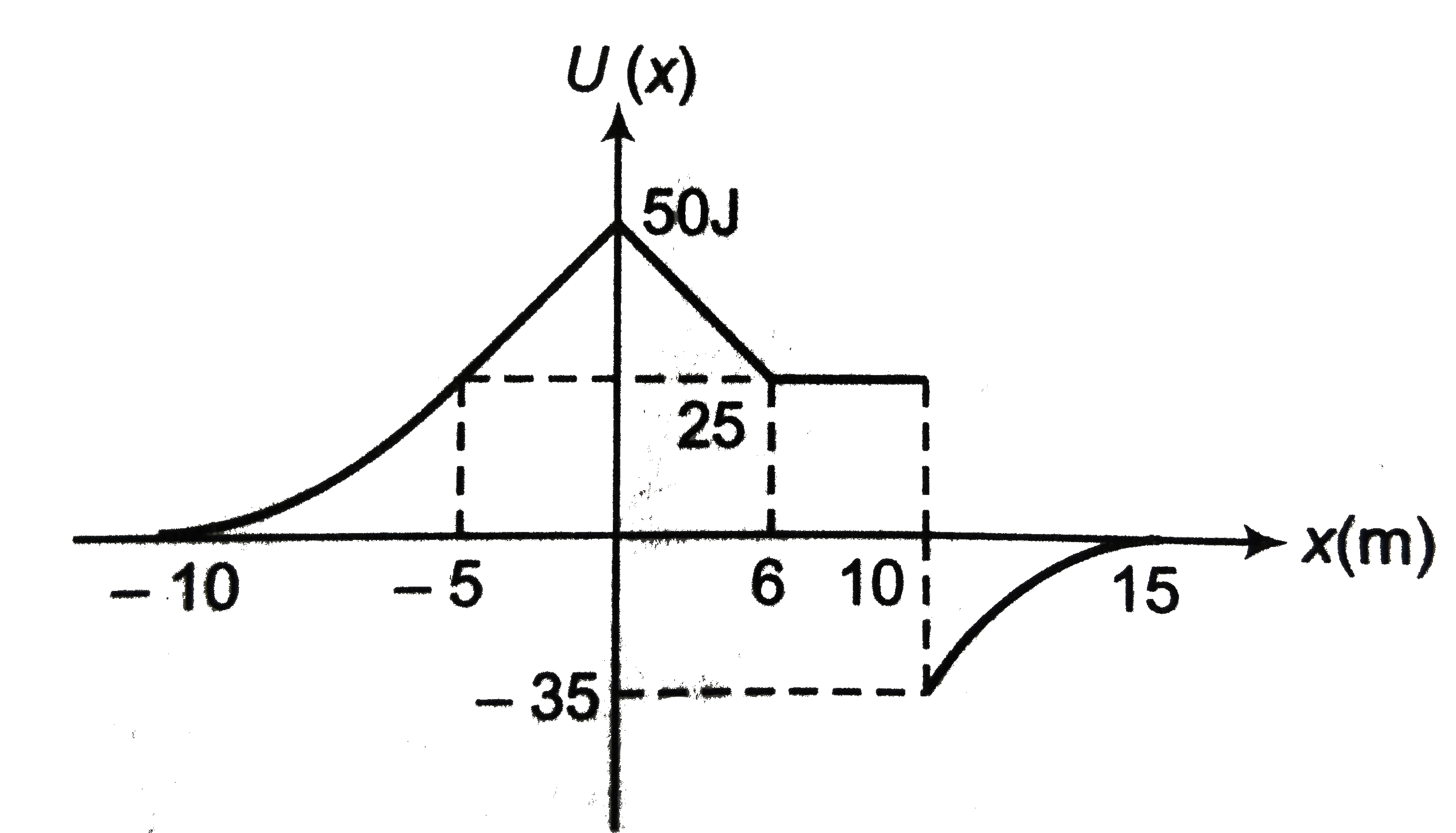
If total mechanical energy of the particle is −40J, then it can be found in region.
View SolutionThe figure shows the variation of potential energy of a particle as a function pf x, the x-coordination of the region. It has been assumed that potential energy depends only on x. For all other values x,U is zero. i.e. forx<−10 and x>15,U=0.
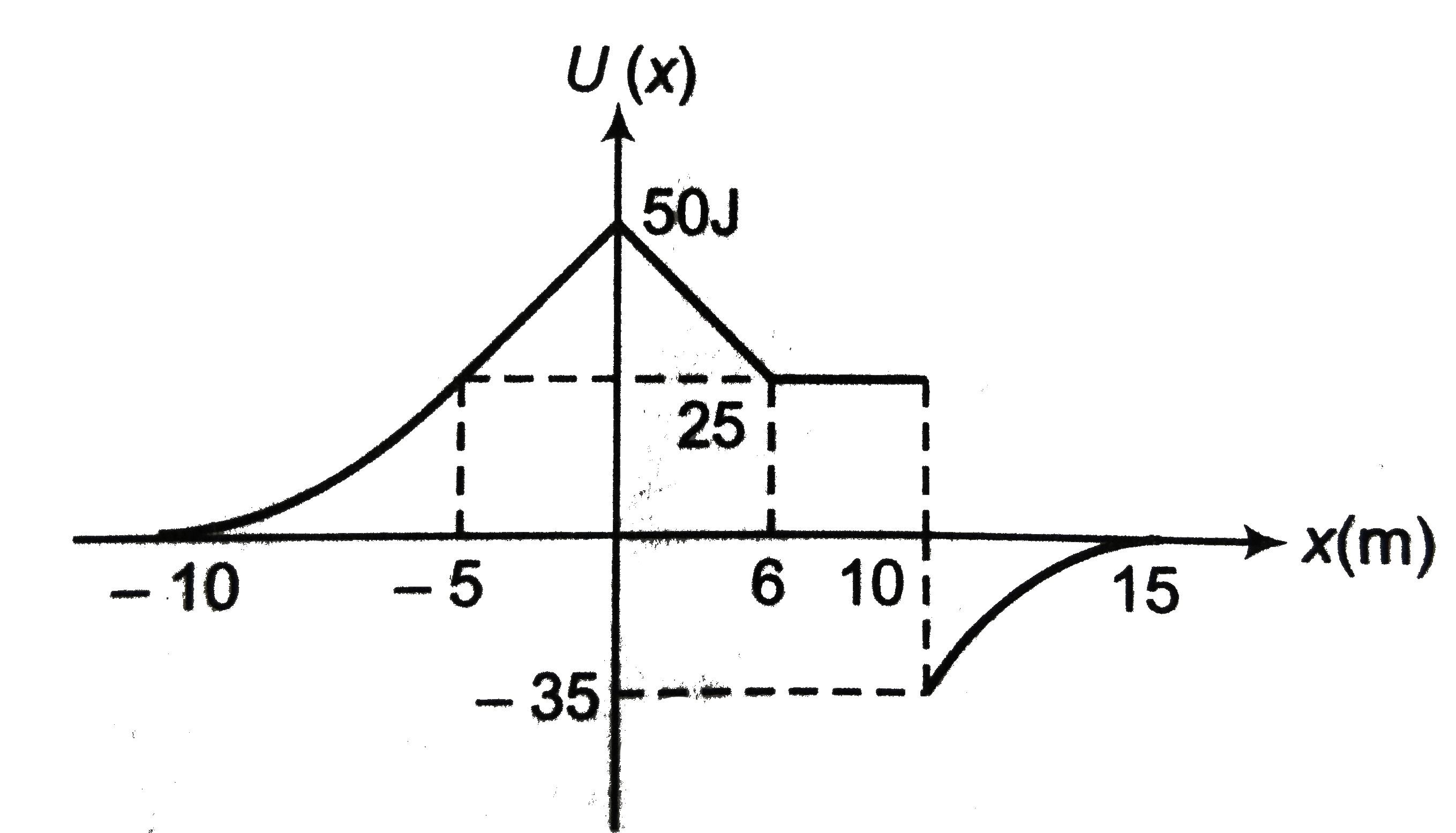
If total mechanical energy of the particle is 25J, then it can found in the region
View SolutionPotential energy curve U of a particle as function of the position of a particle is shown. The particle has total mechanical energy E of 3.0 joules. Then select correct alternative.
View SolutionThe variation of potential energy of a particle of mass m = 5kg to its x-coordinate . The particle moves under the effect of this conservative force only along the x-axis. Then, choose the correct option.
View SolutionPotential energy of a particle is related to x coordinate by equation x2−2x . Particle will be in stable equilibrium at :
View Solution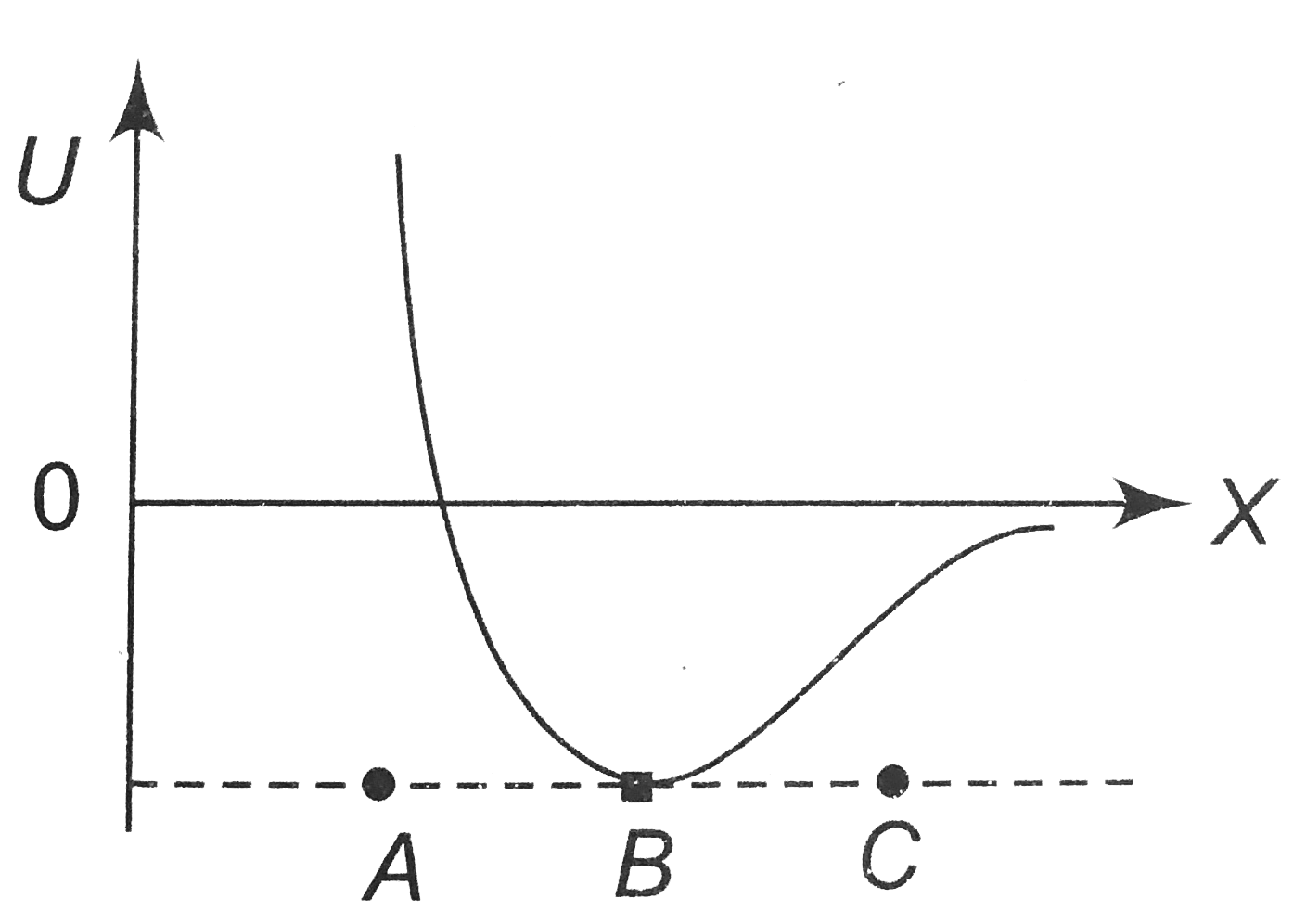
The potential energy U between two molecules as a function of the distance X between them has been shown in the figure. The two molecules are
View Solution
The potential energy U between two molecules as a function of the distance X between them has been shown in the figure. The two molecules are
View SolutionThe potential energy of a particle varies with position X according to the relationU(x)=[(X33)−(3X22)+2X] then
View SolutionFigure shows a plot of the potential energy as a function of x for a particle moving along the x-axis. Which of the following statement(s) is/are true?
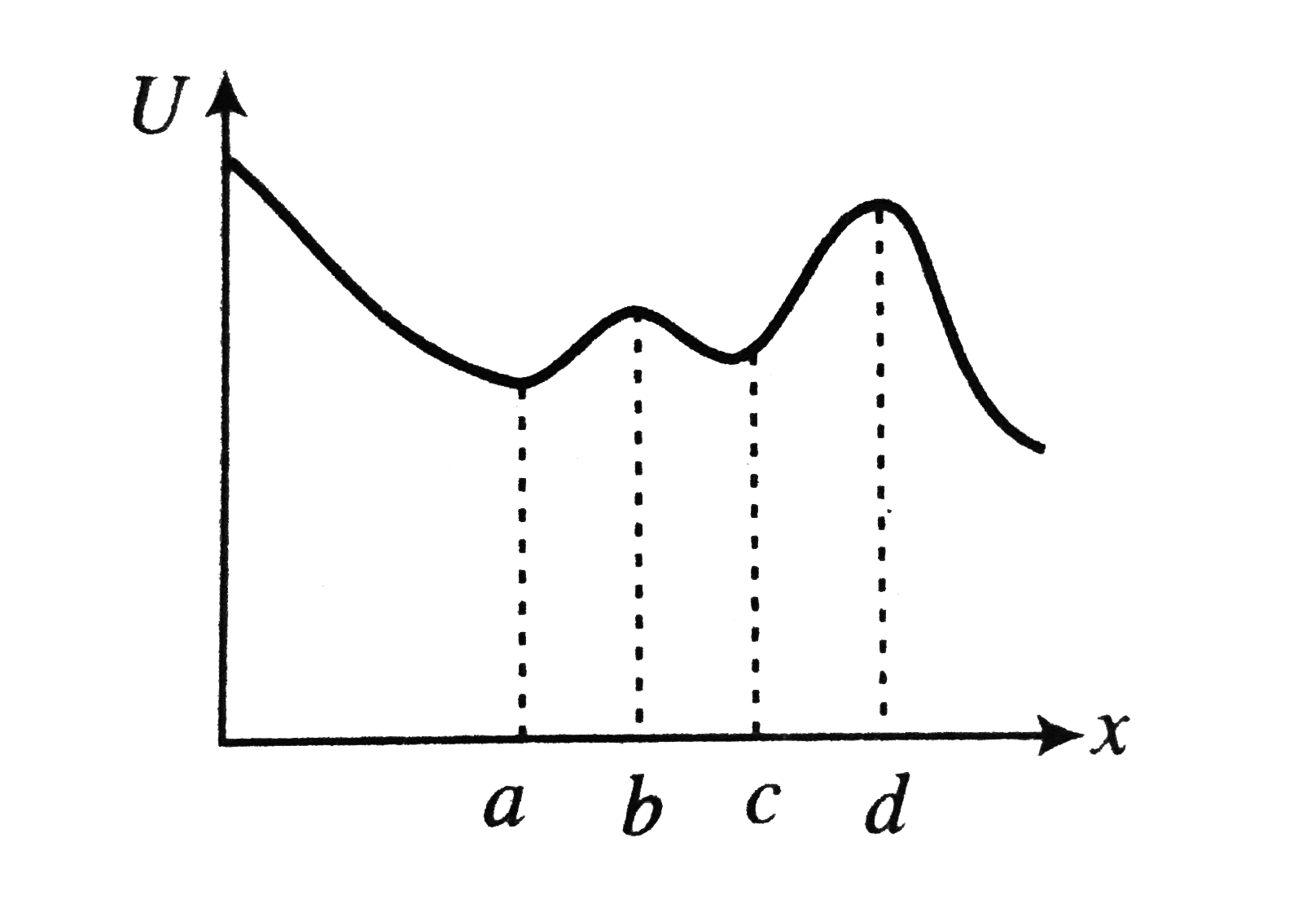
View SolutionFigure shows a plot of the potential energy as a function of x for a particle moving along the x-axis. Which of the following statement(s) is/are true?

View Solution
