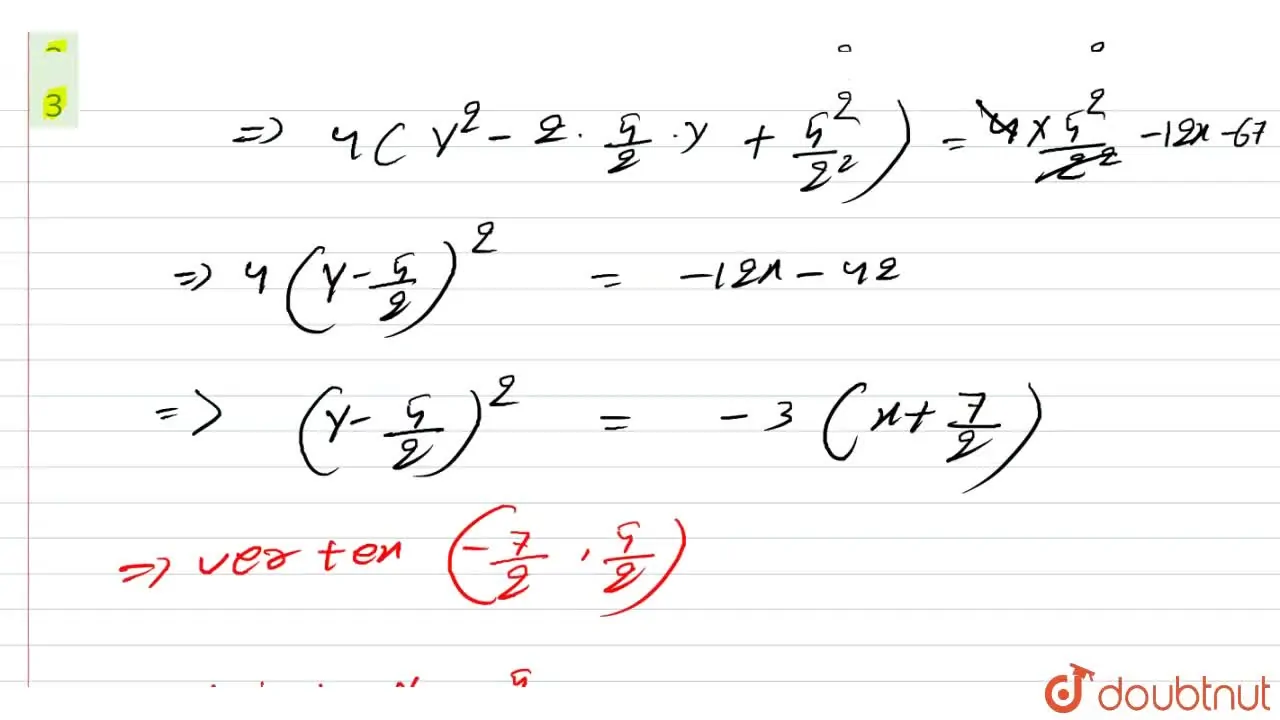The length of the latus rectum of the parabola 4y2+12x−20y+67=0 is
2
1
8
3
The correct Answer is:D
Step by step video & image solution for The length of the latus rectum of the parabola 4y^(2)+12x-20y+67=0 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
The length of the latus rectum of the parabola x2=−28y is
View SolutionI : The length of the latus rectum of the parabola y2+8x−2y+17=0 is 8 .
II: The focal distance of the point (9,6) on the parabola y2=4x is 10View SolutionThe length of the latus - rectum of the parabola 4y2+2x−20y+17=0 is
View SolutionThe length of the latus rectum of the parabola y2+8x−2y+17=0 is a.2 b. 4 c. 8 d. 16
View SolutionFind the length of the latus rectum of the parabola x2=−8y.
View SolutionThe length of latus rectum of the parabola 4y2+2x−20y+17=0 is (a) 3 (b) 6 (c) 12 (d) 9
View SolutionFind the length of latus rectum of the parabola y2=−10x
View SolutionThe length of the latus rectum of the parabola x2−6x+5y=0 is
View SolutionThe length of the latus rectum of the hyperbola x2−4y2=4 is
View SolutionThe equation of the latus rectum of the parabola x2−12x−8y+52=0 is
View Solution