ABCD
is a parallelogram and E and F
are the centroids of
triangles ABD and BCD
respectively, then EF=
(a)AE
(b) BE
(c) CE
(d)
DE
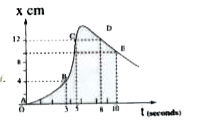
(a) As the particle moves from A to E, is the initial point and E is the final point.
The slope of the line drawn from A to E
i.e., ΔxΔt gives the average velocity during that interval of time.
The displacement Δx is
XE−XA=10cm-0cm=+10cm
The time interval ΔtEA=tE−tA=10S.
∴ During this interval average velocity
¯¯¯V=ΔxΔt=+10cm10S=+1cms−1
(b)During the interval B to E. the displacement
Δx=xE−xB=10cm−4cm=6cm and
Δt=tE−tB=10s−3s=7s.
Therefore Average velocity ¯¯¯V=ΔxΔt=6cm7s
=+0.857 cms−1=0.86cms−1
(c) During the interval C to E,the displacement
Δx=XE−Xc=10cm0−12cm=2cm nd
Δt=tE−tc=10s−5s=5s
∴¯v=ΔxΔt=−2cm5s=−0.4cms−1
(d)During the interval D to E,
the displacement
Δx=xE−xD=10cm−12cm=−2cm
and the time interval
Δt=t−(E)−tD=10s-8s=2
∴¯v=(v)=Δxδt=−2cm2s=−1cms−1
(e)During the interval C to D.the displacement
Δx−xD−xc=12cm 12 cm=0
and the time interval
Δt=tD−tc=8s-5s=3s
∴ The average velocity
¯v=ΔxΔt=0m3s=0ms−1
(The particle has reached the same position during these 3s.The average velocity is zero because the displacement is zero).
Similar Questions
In Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE trisect (divide into three equal parts) the diagonal BD .
View SolutionABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP=PH
View SolutionABCD is a parallelogram and E is the mid-point of BC, DE and AB when produced meet at F. Then AF=
View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(△ADF)=ar(△DCE).
View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(△ADF)=ar(△DCE).
View SolutionABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE=BF=CG=DH. Prove that EFGH is square.
View SolutionABCD is a parallelogram. If AB is produced to E such that BE=AB . Prove that ED bisects BC.
View SolutionABCD is a trapezium with parallel sides AB=a and DC=b. If E and F are mid-points of non-parallel sides AD and BC respectively, then the ratio of areas of quadrilaterals ABFE and EFCD is: a:b (b) (a+3b):(3a+b) (3a+b):(a+3b) (d) (3a+b):(3a+b)
View SolutionABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE=BF=CG=DH. Prove that EFGH is square.
View SolutionAD and BE are respectively altitudes of ABC such that AE=BD. Prove that AD=BE.
View Solution