A mass M kg is suspended by a weightless string. The horizontal force required to hold the mass at 60∘ with the vertical is
Mg
Mg√3
Mg(√3+1)
Mg√3
The correct Answer is:B
To solve the problem of finding the horizontal force required to hold a mass M kg suspended by a weightless string at an angle of 60∘ with the vertical, we can follow these steps:
Step 1: Understand the Forces Acting on the Mass
The mass M experiences three forces:
1. The weight W=Mg acting downwards.
2. The tension T in the string acting along the string.
3. The horizontal force F acting horizontally.
Step 2: Draw a Free Body Diagram
Draw a diagram showing:
- The weight W acting vertically downward.
- The tension T acting at an angle of 60∘ to the vertical.
- The horizontal force F acting horizontally.
Step 3: Resolve the Tension into Components
The tension T can be resolved into two components:
- Vertical component: Tcos(60∘)
- Horizontal component: Tsin(60∘)
Step 4: Set Up the Equations
For the mass to be in equilibrium:
1. The vertical forces must balance:
Tcos(60∘)=Mg
2. The horizontal forces must balance:
F=Tsin(60∘)
Step 5: Solve for Tension T
From the vertical forces equation:
Tcos(60∘)=Mg
Since cos(60∘)=12:
T⋅12=Mg⟹T=2Mg
Step 6: Substitute T into the Horizontal Force Equation
Now substitute T into the horizontal force equation:
F=Tsin(60∘)
Since sin(60∘)=√32:
F=(2Mg)⋅√32=Mg√3
Step 7: Conclusion
The horizontal force required to hold the mass at 60∘ with the vertical is:
F=Mg√3
Final Answer
Thus, the required horizontal force is F=Mg√3.
---
The mass M experiences three forces:
1. The weight W=Mg acting downwards.
2. The tension T in the string acting along the string.
3. The horizontal force F acting horizontally.
Draw a diagram showing:
- The weight W acting vertically downward.
- The tension T acting at an angle of 60∘ to the vertical.
- The horizontal force F acting horizontally.
The tension T can be resolved into two components:
- Vertical component: Tcos(60∘)
- Horizontal component: Tsin(60∘)
For the mass to be in equilibrium:
1. The vertical forces must balance:
Tcos(60∘)=Mg
2. The horizontal forces must balance:
F=Tsin(60∘)
From the vertical forces equation:
Tcos(60∘)=Mg
Since cos(60∘)=12:
T⋅12=Mg⟹T=2Mg
Now substitute T into the horizontal force equation:
F=Tsin(60∘)
Since sin(60∘)=√32:
F=(2Mg)⋅√32=Mg√3
The horizontal force required to hold the mass at 60∘ with the vertical is:
F=Mg√3
Thus, the required horizontal force is F=Mg√3.
Topper's Solved these Questions
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:EXERCISE-3 (Motion in a plane)
Explore 5 Videos
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:EXERCISE-3 (Relative velocity)
Explore 5 Videos
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:EXERCISE-3 (Parallelogram law, triangle law, polygon law)
Explore 4 Videos
- MAGNETISMBook:AAKASH SERIESChapter:MAGNETISMExercise:ADDITIONAL EXERCISE
Explore 22 Videos
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:QUESTION FOR DESCRIPTIVE ANSWER
Explore 7 Videos
Similar Questions
A mass of M kg is suspended by a weightless string. The horizontal force required to displace it until string makes an angle of 45∘ with the initial vertical direction is:
View SolutionA bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
Net acceleration of the bob at this instant is
View SolutionA bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
Upto what maximum height will the bob rise with respect to the bottommost point ?
View SolutionA body of mass 10 kg is suspended by a string and is pulled a side with a horizontal force of 49 N. Find the tension in the string, if the body is in equilibrium under these forces.
View SolutionA heavy particle of mass 1kg suspended from a massless string attached to a roof. A horizontal force F is applied to the particle such that in the equilibrium position the string makes and angle 30∘ with the vertical. The magnitude of the force F equals
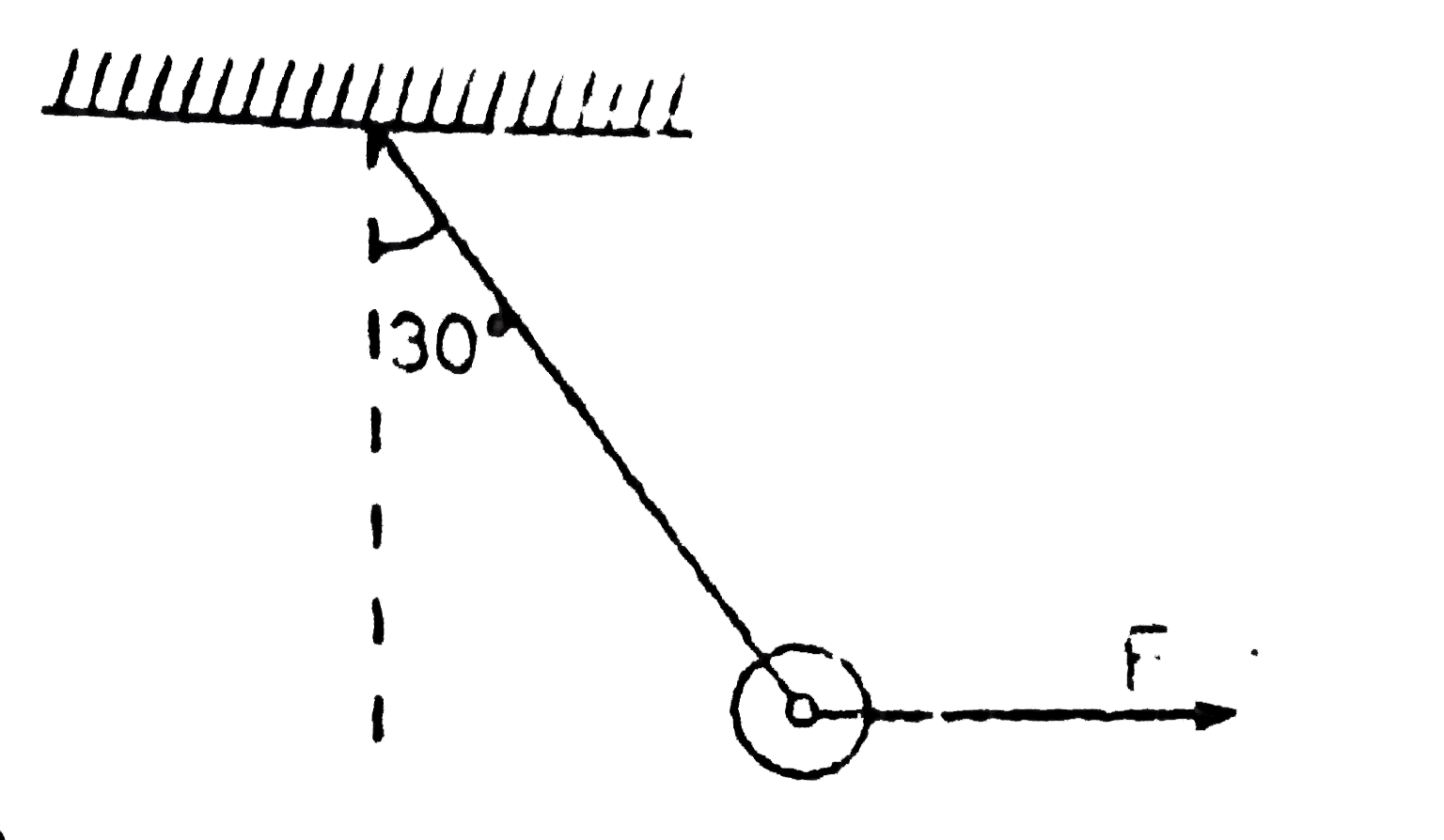 .
.
View SolutionA body of mass 1.0 kg is suspended from a weightless spring having force constant 600Nm−1. Another body of mass 0.5 kg moving vertically upwards hits the suspended body with a velocity of 3.0ms−1 and gets embedded in it. Find the frequency of oscillations and amplitude of motion.
View SolutionA mass of 10 kg is suspended vertically by a rope from the roof. When a horizontal force is applied on the rope at some point, the rope deviated at an angle of 45∘ at the roof point. If the suspended mass is at equilibrium, the magnitude of the force applied is (g=10ms−2)
View SolutionA mass of 10 kg is suspended vertically by a rope from the roof. When a horizontal force is applied on the rope at some point, the rope deviated at an angle of 45∘ at the roof point. If the suspended mass is at equilibrium, the magnitude of the force applied is (g=10ms−2)
View SolutionA car is moving with constant speed of 10m/s on a horizontal circular path of radius 10√3m . A bob of mass m suspended through a light string from the roof of the car. What is the angle made by the string with the vertical if the bob is stationary with respect to the car? (g = 10 m/s2)
View SolutionA bullet of mass 20 g travelling horizontally at 100ms−1 gets embedded at the centre of a block of wood of mass 1kg, suspended by a light vertical string of 1m in length. Calculate the maximum inclination of the string to the vertical.
View Solution

