The displacement of a particle executing simple harmonic motion is given by y=4sin(2t+ϕ). The period of oscillation is
ii only
ii and ii only
iii only
iii and iv only
The correct Answer is:C
Step by step video & image solution for The displacement of a particle executing simple harmonic motion is given by y = 4 sin(2t + phi). The period of oscillation is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- UNITS AND MEASUREMENTSBook:AAKASH SERIESChapter:UNITS AND MEASUREMENTSExercise:EXERCISE- 1 B
Explore 28 Videos
- UNITS AND MEASUREMENTSBook:AAKASH SERIESChapter:UNITS AND MEASUREMENTSExercise:EXERCISE -2
Explore 56 Videos
- UNITS AND MEASUREMENTSBook:AAKASH SERIESChapter:UNITS AND MEASUREMENTSExercise:PROBLEM
Explore 50 Videos
- UNITS AND MEASUREMENTBook:AAKASH SERIESChapter:UNITS AND MEASUREMENTExercise:PRACTICE EXERCISE
Explore 45 Videos
- WAVE MOTIONBook:AAKASH SERIESChapter:WAVE MOTIONExercise:PRACTICE SHEET ADVANCED (INTEGER TYPE QUESTIONS)
Explore 10 Videos
Similar Questions
Knowledge Check
The displacement of a particle executing simple harmonic motion is given by
x=3sin(2πt+π4)
where x is in metres and t is in seconds. The amplitude and maximum speed of the particle isA3m, 2πms−1B3m, 4πms−1C3m, 6πms−1D3m, 8πms−1The differential equation of a particle executing simple harmonic motion along y-axis is
Ad2ydt2+ω2y=0Bd2ydt2+ω2y2=0Cd2ydt2−ω2y=0Ddydt+ωy=0
The plot of velocity (v) versus displacement (x) of a particle executing simple harmonic motion is shown in figure. The time period of oscillation of particle is :-
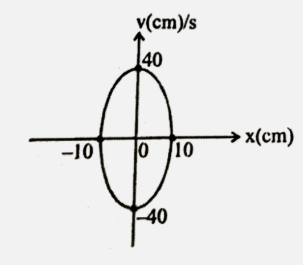
View SolutionThe displacement of a particle of mass 3g executing simple harmonic motion is given by x=3sin(0.2t) in SI units. The kinetic energy of the particle at a point which is at a displacement equal to 13 of its amplitude from its mean position is
View SolutionThe acceleration-displacement graph of a particle executing simple harmonic motion is shown in the figure. The frequency of oscillation is
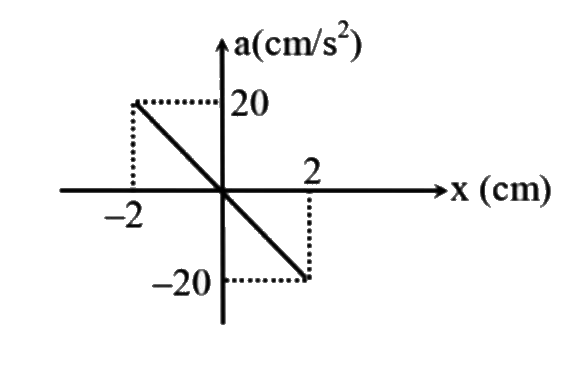
View Solution(b) The displacement of a particle executing simple harmonic motion is given by the equation y=0.3sin20π(t+0.05) , where time t is in seconds and displacement y is in meter. Calculate the values of amplitude, time period, initial phase and initial displacement of the particle.
View SolutionThe displacement of a particle executing simple harmonic motion is given by y=A0+Asinωt+Bcosωt. Then the amplitude of its oscillation is given by
View SolutionFor a particle executing simple harmonic motion, the acceleration is -
View Solution

