A block A of mass 8 kg is placed on a frictionless horizontal table. A thread tied to it passes over a frictionless pulley and carries a body B of mass 2 kg at the other end. Find the acceleration of the system. Also find the tension in the thread. If the thread is cut into two and tied to the ends of a spring of forceconstant 1600N/m, find the amount of stretching of the spring. Neglect the mass of thread and of spring (g=9.8m/s2)
To solve the problem step by step, we will first analyze the forces acting on the two masses and then apply Newton's second law to find the acceleration and tension in the system. Finally, we will calculate the stretching of the spring when the thread is cut.
Step 1: Identify the masses and forces
- Mass of block A (m1) = 8 kg (on the table)
- Mass of block B (m2) = 2 kg (hanging)
- Gravitational acceleration (g) = 9.8 m/s²
Step 2: Write the equations of motion
For block B (mass m2):
- The forces acting on m2 are the gravitational force (m2 * g) downward and the tension (T) upward.
- According to Newton's second law:
m2⋅g−T=m2⋅a(1)
For block A (mass m1):
- The only force acting on m1 is the tension (T) since the table is frictionless.
- According to Newton's second law:
T=m1⋅a(2)
Step 3: Combine the equations
Now, we can add equations (1) and (2):
m2⋅g−T+T=m2⋅a+m1⋅a
This simplifies to:
m2⋅g=(m1+m2)⋅a
Now, we can solve for acceleration (a):
a=m2⋅gm1+m2
Step 4: Substitute the values
Substituting the known values:
a=2⋅9.88+2=19.610=1.96m/s2
Step 5: Find the tension in the thread
Using equation (2):
T=m1⋅a
Substituting the values:
T=8⋅1.96=15.68N
Step 6: Calculate the stretching of the spring
When the thread is cut and tied to a spring with a spring constant (k) of 1600 N/m, the tension in the spring will be equal to the tension we calculated earlier (T = 15.68 N).
Using Hooke's Law:
T=k⋅x⇒x=Tk
Substituting the values:
x=15.681600=0.0098m
Final Answers:
- The acceleration of the system is 1.96 m/s².
- The tension in the thread is 15.68 N.
- The amount of stretching of the spring is 0.0098 m.
- Mass of block A (m1) = 8 kg (on the table)
- Mass of block B (m2) = 2 kg (hanging)
- Gravitational acceleration (g) = 9.8 m/s²
For block B (mass m2):
- The forces acting on m2 are the gravitational force (m2 * g) downward and the tension (T) upward.
- According to Newton's second law:
m2⋅g−T=m2⋅a(1)
- The only force acting on m1 is the tension (T) since the table is frictionless.
- According to Newton's second law:
T=m1⋅a(2)
Now, we can add equations (1) and (2):
m2⋅g−T+T=m2⋅a+m1⋅a
This simplifies to:
m2⋅g=(m1+m2)⋅a
Now, we can solve for acceleration (a):
a=m2⋅gm1+m2
Substituting the known values:
a=2⋅9.88+2=19.610=1.96m/s2
Using equation (2):
T=m1⋅a
Substituting the values:
T=8⋅1.96=15.68N
When the thread is cut and tied to a spring with a spring constant (k) of 1600 N/m, the tension in the spring will be equal to the tension we calculated earlier (T = 15.68 N).
T=k⋅x⇒x=Tk
Substituting the values:
x=15.681600=0.0098m
- The acceleration of the system is 1.96 m/s².
- The tension in the thread is 15.68 N.
- The amount of stretching of the spring is 0.0098 m.
Similar Questions
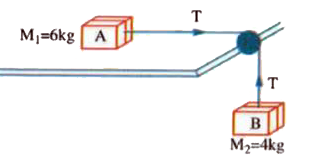
A block A of mass 6kg is applied on a frictionless table. A thread tied to it passes over a frictionless pulley and carries a body B of mass 4kg at the other end. Find the acceleration of the system and tension in the thread (given g=10ms−2)
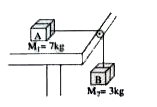
View SolutionA block A of mass 7Kg is placed on a frictionless table. A thread tied to it passes over frictionless pulley and carries a body B of mass 3 Kg at the other end. The acceleration of the system is ......... (m/s)(Given g=10ms−2 )
View SolutionA block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
View SolutionA block of mass 20 kg is set into motion on a frictionless horizontal surface with the help of massless smooth pulley and rope as shown in the figure. Find the acceleration of the pulley
_PHY_E05_192_Q05.png)
View SolutionA block of mass 2 kg placed on a long frictionless horizontal table is pulled horizontally by a constant foerce F. It is found to move 10 m in the first two seconds. Find the magnitude of F.
View SolutionTwo masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View SolutionTwo masses 2 kg and 4 kg are connected at two ends of light inextensible string passing over a frictionless pulley . If the masses are released , then find the accelaration of the masses and the tension in the string .
View SolutionA block of mass M placed on a frictionless horizontal table is pulled by another block of mass m hanging vertically by a massless string passing over a frictionless pulley. The tension in the string is :
View SolutionA block of mass of 20kg is set into motion on a frictionless horizontal surface with the help of massless smooth pulley and rope as shown in figure.Find the acceleration of the pulley
_PHY_E05_034_Q01.png) .jpg
.jpg
View Solution(1) Find the acceleration of centre of mass of the system shown.
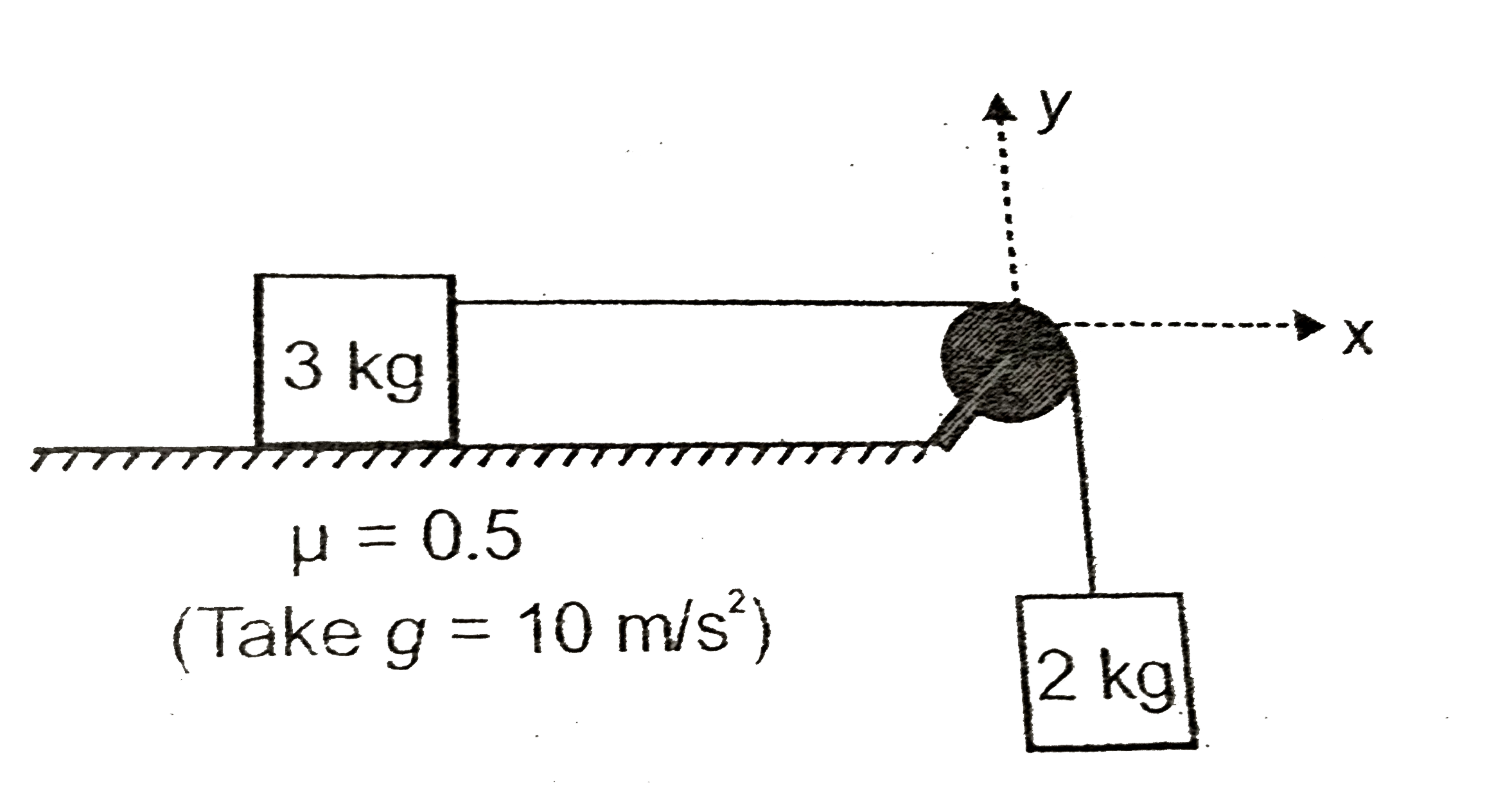
(ii) Find the normal reaction applied by the pulley on the thread.
View Solution

