A block of mass is attached to a spring of force constant whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is


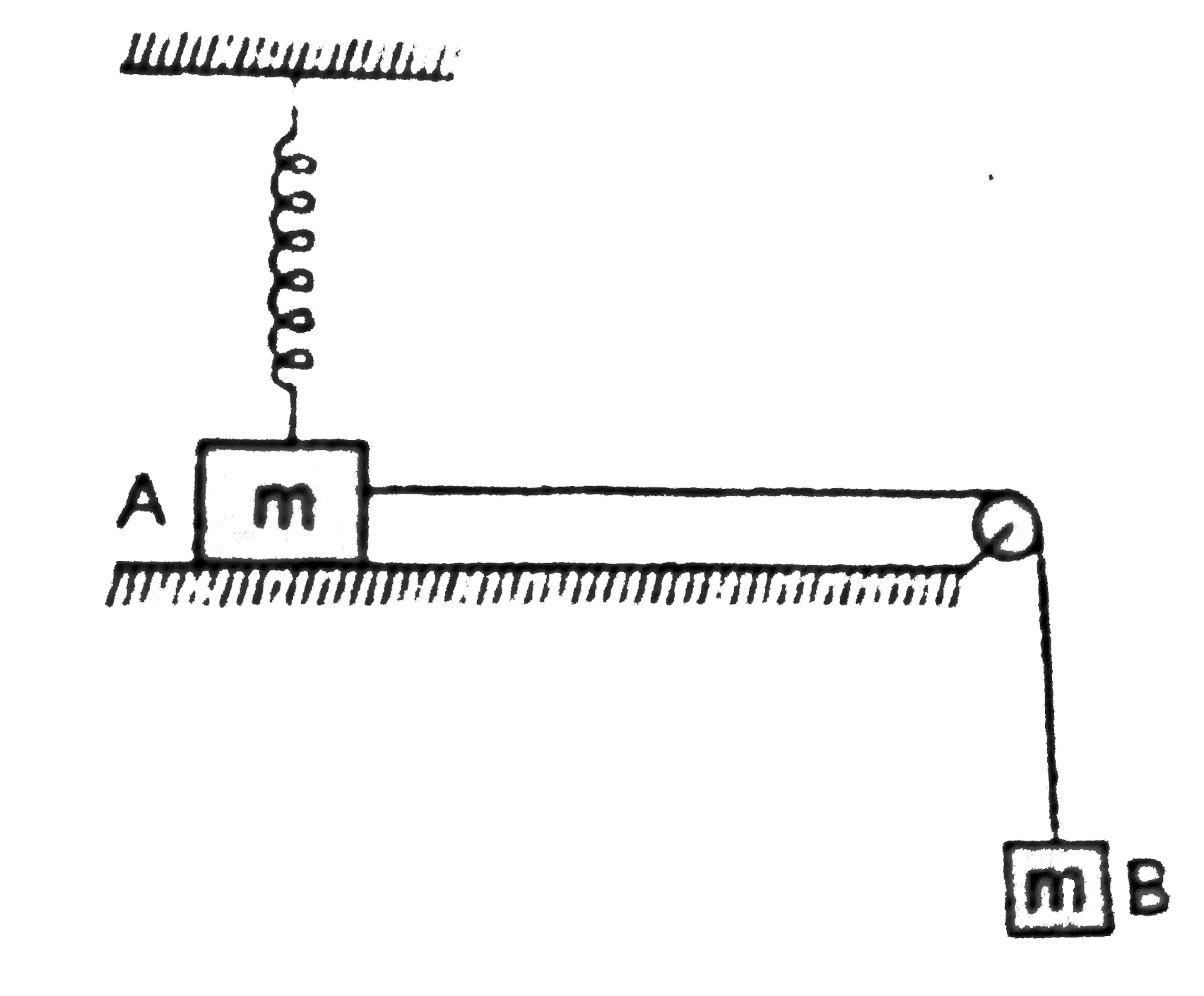
Due to weight of block B, it moves down and pulls the block A now as block A and B move, spring gets stretched and becomes inclined as its lower end is attached to the block A. It will break off from the ground below it when the vertical component of the spring force on block A will balance its weight mg Let it happens
when A moves by a distances as shown in figure.
At this instant let the spring be inclined at an angle with the vertical
If the stretch in the spring at this instant is x, then it is given as
or ........... (1)
If mass A breaks off from ground below it , we have
From equation (1) and (2) substituting the value of x, we get
At this instant the distance travelled by mass A and B is given by
Similar Questions
Find the maximum tension in the spring if initially spring at its natural length when block is released from rest.

View SolutionA block of mass m is attached with a spring in vertical plane as shown in the figure. If initially spring is in its natural length and the block is released from rest, then maximum extension in the spring will be
View SolutionA block of mass m is connected to a spring (spring constant k). Initially the block is at rest and the spring is in its natural length. Now the system is released in gravitational field and a variable force F is applied on the upper end of the spring such that the downward acceleration of the block is given as a=g−αt, where t is time elapses and α=1m/s2, the velocity of the point of application of the force is:
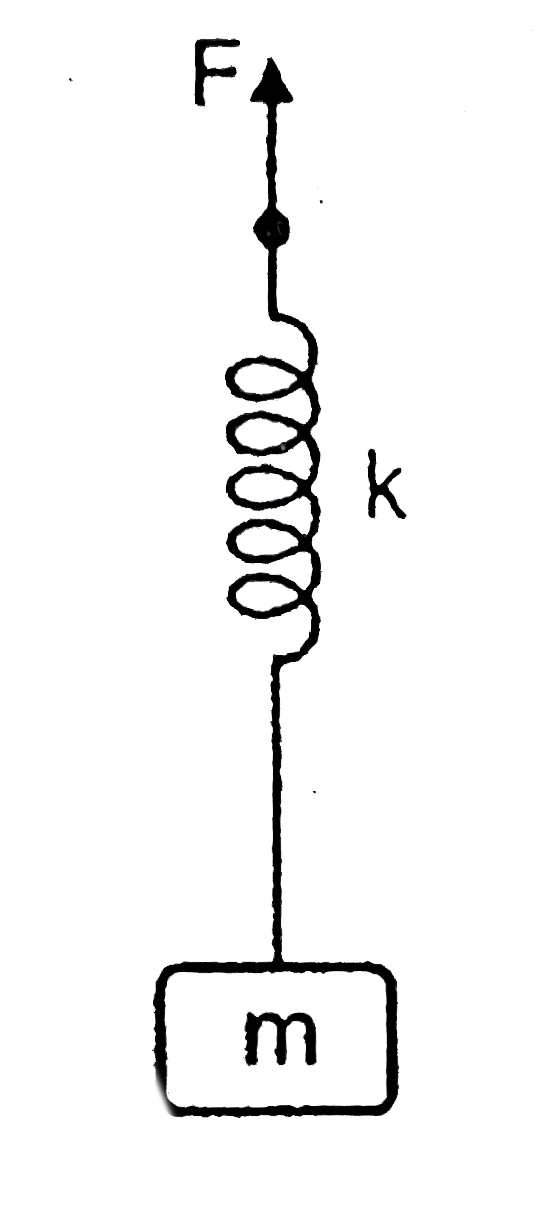
View SolutionFigure shows two block A and B, each having a mass of 320 g connected by a light string passing over a smooth light pulley. The horizontal surface on which the block A can slide is smooth. The block A is attached to spring constant 40N/m whose other end is fixed to a support 40 cm above the horizontal surface. Initially, the spring is vertical and unstretched when the system is released to move. Find the velocity of the block A at the instant it breaks off the surface below it. Take g=10m/s2 .
View SolutionA block of mass m is attached to a massless spring of force constant k, the other end of which is fixed from the wall of a truck as shown in figure. The block is placed over a smooth surface and initially the spring is unstretched. Suddenly the truck starts moving towards right with a constant accleration a0. As seen from the truck

View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

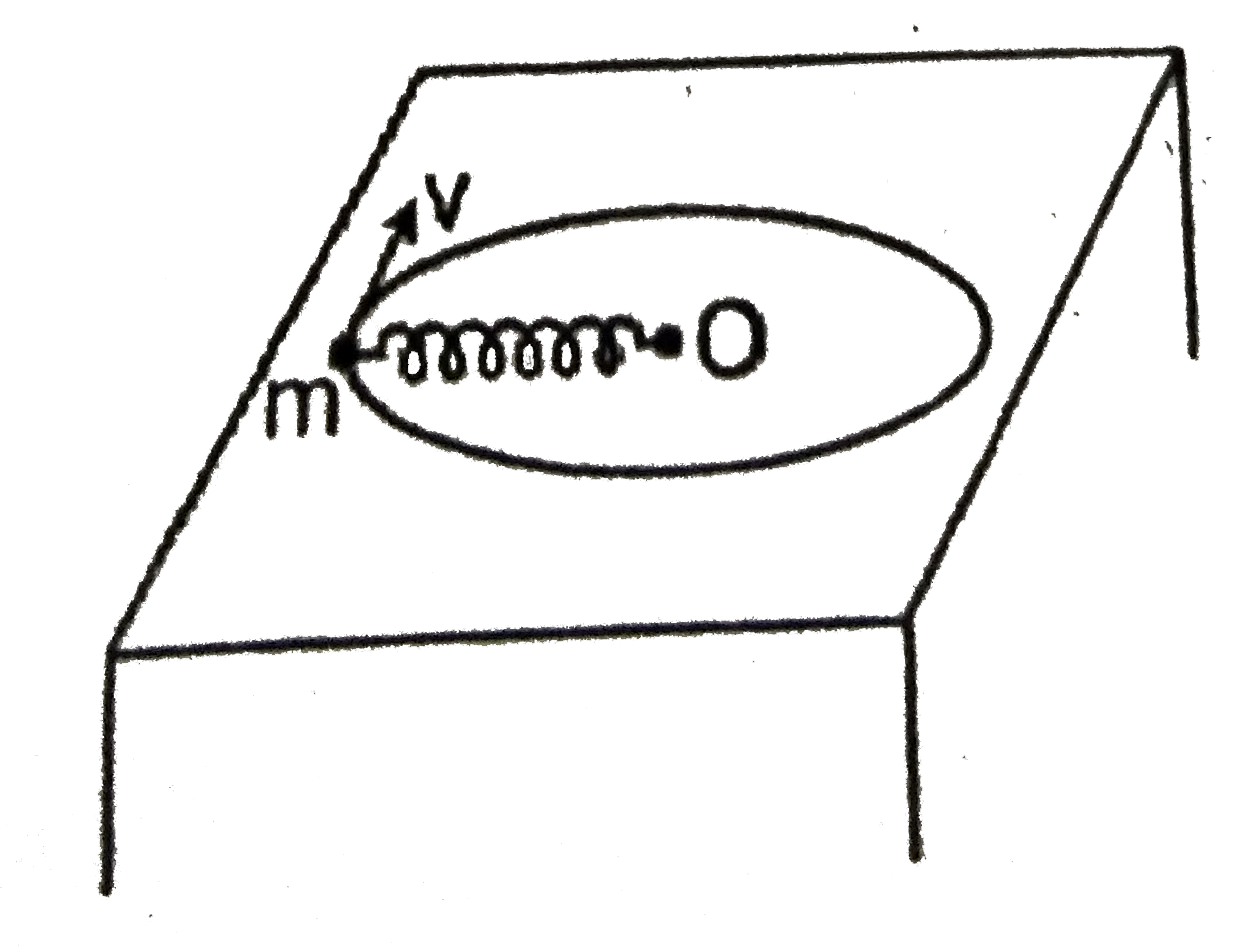
View SolutionMass m is connected with an ideal spring of natural length l whose other end is fixed on a smooth horizontal table. Initially spring is in its natural length l. Mass m is given a velocity 'v' perpendicular to the spring and released . The velocity perpendicular to the spring when its length l+x , will be
View SolutionA block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionA block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
View Solution
