A ball falls freely form a height onto and smooth inclined plane forming an angle a with the horizontal. Find the ratio of the distance between the points at which the jumping ball strikes the inclined plane. Assume the impacts to be elastic.
The situation is shown in Fig.
Let the ball rebound from point A and return to the plane at point B, moving along the trajectory shown in diagram.
Let, AB=l
Velocity of rebound at point A,v=√2gh
Velocity component perpendicular to plane = vcosα
Velocity component along the plane =vsinalpah
Retardation perpendicular to plane = g sin α
Acceleration along the plane = g sin α
If the ball comes to rest at this highest point after time t, then (vcosαgcosα.t) = 0 or t=vg
Time of flight of the ball, T=2t=2vg
Range of the ball along the plane,
l(vsinα)T+12 . g sin alpha 4v2g2
=2v2gsinα+2v2gsinα
(becuaev=√2gh) ∴l=8hsinα
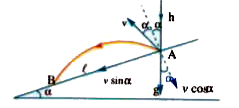
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - SHORT ANSWER TYPE QUESTIONS
6 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
10 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-3 (Circular Motion)
7 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
Similar Questions
A ball starts falling freely from a height h from a point on the inclined plane forming an angle α with the horizontal as shown. After collision with the incline it rebounds elastically off the plane. Then it again strikes the incline at

View SolutionA block is placed on a smooth inclined plane at an angle 'θ' to the horizontal. The acceleration must the plane be moved horizontally so that the block to fall freely is
View SolutionA trolley containing a liquid slides down a smooth inclined plane of angle α with the horizontal. Find the angle of inclination θ of the free surface with the horizontal.

View SolutionA uniform solid cyinder of radius R=15cm rolls over a horizontal plane passing into an inclined plane forming an ange α=30∘ with the horizontal. Find the maximum value of the velocity v0 which still permits the cylinder to roll on the inclined plane section without a jump. (The sliding is asumed to be absent).

View SolutionA ball is projected form a point A on a smooth inclined plane which makes an angle a to the horizontal. The velocity of projection makes an angle θ with the plane upwards. If on the second bounce the ball is moving perpendicular to the plane, find e in terms of α and θ. Here e is the coefficient of restitution between the ball and the plane.
View SolutionA ball is dropped from a height h on a inclined plane, ball collides elastically with the first plane. Find the value of 'h' (in meter) so that it strikes perpendicular on the second inclined plane.
View SolutionA ball is projected horizontally with a speed v from the top of the plane inclined at an angle 45∘ with the horizontal. How far from the point of projection will the ball strikes the plane?
View SolutionA projectile si thrown with velocity of 50m/s towards an inclined plane from ground such that is strikes the inclined plane perpendiclularly. The angle of projection of the projectile is 53∘ with the horizontal and the inclined plane is inclined at an angle of 45∘ to the horizonta..

(a) Find the time of flight.
(b) Find the distance between the point of projection and the foot of inclined plane.
View SolutionA particle is projected with a velocity u making an angle θ with the horizontal. The instantaneous power of the gravitational force
View SolutionA particle is projected up an inclined plane of inclination β at an elevation ∝ to the horizontal. Find the ratio between tan∝andtanβ, if the particle strikes the plane horizontally.
View Solution
