A cannon and a target are 5.10Km apart and located at the same level. How soon will the shell launched with the initial velocity 240m/s reach the target in the absence of air drag?
To solve the problem of how soon the shell launched from the cannon will reach the target, we can follow these steps:
Step 1: Convert the distance to meters
The distance between the cannon and the target is given as 5.10 km. To work in consistent units, we convert this distance to meters:
r=5.10km=5.10×1000m=5100m
Hint: Always ensure that all units are consistent when solving physics problems.
Step 2: Write down the known quantities
We have the following known quantities:
- Distance to target, r=5100m
- Initial velocity, u0=240m/s
- Acceleration due to gravity, g=9.8m/s2
Hint: List all known quantities clearly to avoid confusion later in the calculations.
Step 3: Use the range formula
The formula for the range R in projectile motion is given by:
R=u20sin2θg
From this, we can rearrange to find sin2θ:
sin2θ=Rgu20
Hint: Familiarize yourself with the projectile motion equations, especially the range formula.
Step 4: Express sinθ in terms of time
The time of flight t for a projectile is given by:
t=2u0sinθg
From this, we can express sinθ:
sinθ=gt2u0
Hint: Remember that time of flight is influenced by the vertical component of the initial velocity.
Step 5: Substitute sinθ into the range equation
Substituting sinθ into the equation for sin2θ:
sin2θ=2sinθcosθ=2(gt2u0)cosθ
This simplifies to:
sin2θ=gtu0cosθ
Setting this equal to the earlier expression for sin2θ:
gtu0cosθ=Rgu20
Cancelling g and u0 gives:
cosθ=Ru0t
Hint: When substituting values, ensure that you maintain the relationships between the trigonometric functions.
Step 6: Use the Pythagorean identity
Using the identity sin2θ+cos2θ=1:
(gt2u0)2+(Ru0t)2=1
Substituting the known values:
(9.8t2×240)2+(5100240t)2=1
Hint: The Pythagorean identity is a powerful tool in projectile motion problems.
Step 7: Solve the equation
This leads to a quadratic equation in terms of t2:
(9.82t2)(2×240)2+(51002)(2402t2)=1
Multiplying through by (2402t2) to eliminate the denominators gives:
9.82t4−2400t2+108340=0
Hint: When dealing with quadratic equations, ensure all terms are correctly arranged.
Step 8: Use the quadratic formula
Using the quadratic formula t2=−b±√b2−4ac2a, we can solve for t2:
t2=2400±√24002−4×9.82×1083402×9.82
Calculating the discriminant and solving gives two possible values for t.
Hint: Always check for both roots when using the quadratic formula; one may be extraneous.
Step 9: Calculate the time
Calculating the values gives:
t≈42.39sort≈24.55s
The smaller time is the one we are interested in since we want to know how soon the shell reaches the target.
Hint: When interpreting the results, consider the context of the problem.
Step 10: Convert to minutes
Finally, converting seconds to minutes:
t≈0.41minutes
Hint: Converting units is often necessary to match the question's requirements.
Final Answer
The shell will reach the target in approximately 0.41 minutes.
The distance between the cannon and the target is given as 5.10 km. To work in consistent units, we convert this distance to meters:
r=5.10km=5.10×1000m=5100m
We have the following known quantities:
- Distance to target, r=5100m
- Initial velocity, u0=240m/s
- Acceleration due to gravity, g=9.8m/s2
The formula for the range R in projectile motion is given by:
R=u20sin2θg
From this, we can rearrange to find sin2θ:
sin2θ=Rgu20
The time of flight t for a projectile is given by:
t=2u0sinθg
From this, we can express sinθ:
sinθ=gt2u0
Substituting sinθ into the equation for sin2θ:
sin2θ=2sinθcosθ=2(gt2u0)cosθ
This simplifies to:
sin2θ=gtu0cosθ
Setting this equal to the earlier expression for sin2θ:
gtu0cosθ=Rgu20
Cancelling g and u0 gives:
cosθ=Ru0t
Using the identity sin2θ+cos2θ=1:
(gt2u0)2+(Ru0t)2=1
Substituting the known values:
(9.8t2×240)2+(5100240t)2=1
This leads to a quadratic equation in terms of t2:
(9.82t2)(2×240)2+(51002)(2402t2)=1
Multiplying through by (2402t2) to eliminate the denominators gives:
9.82t4−2400t2+108340=0
Using the quadratic formula t2=−b±√b2−4ac2a, we can solve for t2:
t2=2400±√24002−4×9.82×1083402×9.82
Calculating the discriminant and solving gives two possible values for t.
Calculating the values gives:
t≈42.39sort≈24.55s
The smaller time is the one we are interested in since we want to know how soon the shell reaches the target.
Finally, converting seconds to minutes:
t≈0.41minutes
The shell will reach the target in approximately 0.41 minutes.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - SHORT ANSWER TYPE QUESTIONS
6 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
10 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-3 (Circular Motion)
7 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
Similar Questions
Two balls of equal masses are thrown upwards, along the same vertical direction at an interval of 2 seconds, with the same initial velocity of 40m/s. Then these collide at a height of (Take g=10m/s2).
View SolutionA cannon of mass 5m (including a shell of mass m) is at rest on a smooth horizontal ground, fires the shell with its barrel at an angle θ with the horizontal at a velocity u relative to cannon. Find the horizontal distance of the point where shell strikes the ground from the initial position of the cannon :-
View SolutionA cannon of mass 1000kg located at the base of an inclined plane fires a shell of mass 50kg in horizontal direction with velocity 180km/h. The angle of inclination of the inclined plane with the horizontal is 45∘. The coefficient of friction between the cannon and inclined plane is 0.5. The maximum height, in metre, to which the cannon can ascend the inclined plane as a result of recoil is
View SolutionA bullet of mass 20 g leaves a riffle at an initial speed 100 m/s and strikes a target at the same level with speed 50 m/s. The amount of work done by the resistance of air will be
View SolutionAn observer having a gun observes a remotely controlled balloon. When he first noticed the balloon, it was at an altitude of 800m and moving vertically upward at a constant velocity of 5m/s. The horizontal displacement of balloon from the observer is 1600m. Shells fired from the gun have an initial velocity of 400m/s at a fixed angle θ(sinθ=3/5and cosθ=4/5). The observer having gun waits ( for some time after observing the balloon ) and fires so as to destroy the balloon. Assume g=10m/s2. Neglect air resistance.
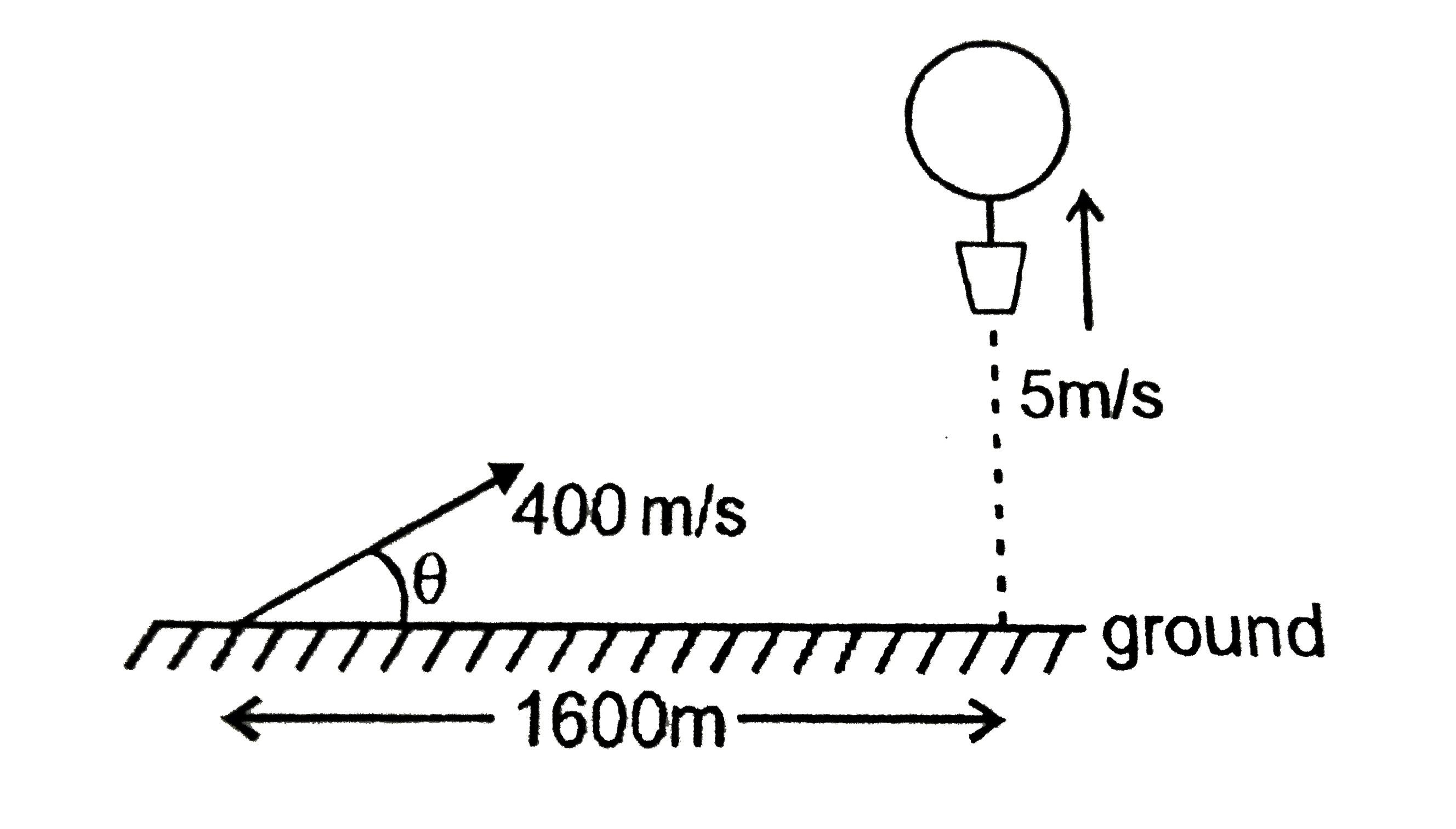
The altitude of the collosion above ground level is
View SolutionAn observer having a gun observes a remotely controlled balloon. When he first noticed the balloon, it was at an altitude of 800m and moving vertically upward at a constant velocity of 5m/s. The horizontal displacement of balloon from the observer is 1600m. Shells fired from the gun have an initial velocity of 400m/s at a fixed angle θ(sinθ=3/5and cosθ=4/5). The observer having gun waits ( for some time after observing the balloon ) and fires so as to destroy the balloon. Assume g=10m/s2. Neglect air resistance.

The flight time of the shell before it strikes the balloon is
View SolutionA car P is moving with a uniform speed 5√3m/s towards a carriage of mass 9 kg at rest kept on the rails at a point B as shown in the figure. The height AC is 120 m. Cannon balls of 1 kg are fired from the car with an initial velocity 100 m/s with respect to the car at an angle 30∘ with the horizontal.

The first cannon ball hits the stationary carriage after a time t0 and sticks to it. Determine t0. (in sec)
View SolutionA projectile is fired vertically from the earth's surface with an initial speed of 10km/s. Neglecting air drag, how high above the surface of earth will it go?
View SolutionA bullet of mass 10g leaves a rifle at an intial velocity of 1000m/s and strikes the earth at the same level with a velocity of 500m/s. The work done in joule to overcome the resistance of air will be
View SolutionA projectille covers a horizontal distance of 6 m, when it reaches 10 m above the level of projection, how farther should if travel horizontally to reach back the same height , if its horizontal range is 20 m ?
View Solution
