Check the correctness of the formula where S is the distance , u is velocity , a is acceleration and t is time.
To check the correctness of the formula S=ut+13at2, we will analyze the components of the equation and compare it with the standard equations of motion.
Step 1: Understand the components of the formula
- S represents the distance traveled.
- u is the initial velocity.
- a is the acceleration.
- t is the time.
Step 2: Compare with standard equations of motion
The standard equation for distance in uniformly accelerated motion is:
S=ut+12at2
This equation states that the distance S is equal to the initial velocity multiplied by time plus half of the acceleration multiplied by the square of time.
Step 3: Identify the discrepancy
In the given formula S=ut+13at2, the term involving acceleration is 13at2 instead of 12at2. This indicates that the formula is incorrect because the coefficient of at2 does not match the standard equation.
Step 4: Conclusion
Since the formula S=ut+13at2 does not align with the established equation of motion, we conclude that it is incorrect.
Summary of the steps:
1. Identify the components of the formula.
2. Compare it with the standard equation of motion.
3. Identify the discrepancy in the coefficient of at2.
4. Conclude that the formula is incorrect.
- S represents the distance traveled.
- u is the initial velocity.
- a is the acceleration.
- t is the time.
The standard equation for distance in uniformly accelerated motion is:
S=ut+12at2
This equation states that the distance S is equal to the initial velocity multiplied by time plus half of the acceleration multiplied by the square of time.
In the given formula S=ut+13at2, the term involving acceleration is 13at2 instead of 12at2. This indicates that the formula is incorrect because the coefficient of at2 does not match the standard equation.
Since the formula S=ut+13at2 does not align with the established equation of motion, we conclude that it is incorrect.
1. Identify the components of the formula.
2. Compare it with the standard equation of motion.
3. Identify the discrepancy in the coefficient of at2.
4. Conclude that the formula is incorrect.
Topper's Solved these Questions
- UNITS AND MEASUREMENTSBook:AAKASH SERIESChapter:UNITS AND MEASUREMENTSExercise:SHORT ANSWER TYPE QUESTIONS
Explore 16 Videos
- UNITS AND MEASUREMENTSBook:AAKASH SERIESChapter:UNITS AND MEASUREMENTSExercise:VERY SHORT ANSWER TYPE QUESTIONS
Explore 24 Videos
- UNITS AND MEASUREMENTBook:AAKASH SERIESChapter:UNITS AND MEASUREMENTExercise:PRACTICE EXERCISE
Explore 45 Videos
- WAVE MOTIONBook:AAKASH SERIESChapter:WAVE MOTIONExercise:PRACTICE SHEET ADVANCED (INTEGER TYPE QUESTIONS)
Explore 10 Videos
Similar Questions
Chek the correctness of the relation, Snth=u+a2(2n−1), where u is initial velocity, a is acceleratin and Snth is the distance travelled by the body in nth second.
View SolutionCheck the correctness of following equation by the method of dimensions :
S=ut+12at2 .
where S is the distance covered bu a body in time t, having initial velocity u and acceleration a.
View SolutionCheck the correctness of the equations (i) s=ut+12at2 (ii) v2=u2+2as using dimensions.
View SolutionA particle starts rotating from rest according to the formula θ=(t2/64)−(t/8) where θ is the angle in radian and t in s . Find the angular velocity and angular acceleration at the end of 4 s .
View SolutionThe motion of a particle along a straight line is described by the function x=(2t−3)2, where x is in metres and t is in seconds. Find
(a) the position, velocity and acceleration at t=2s.
(b) the velocity of the particle at origin.
View SolutionThe motion of a particle along a straight line is described by the function x=(2t−3)2, where x is in metres and t is in seconds. Find
(a) the position, velocity and acceleration at t=2s.
(b) the velocity of the particle at origin.
View Solution(a) Write a equation of motion in different states and derive the relation :
s=u+12a(2t−1)
Where, s is the distance covered in tth second, u is initial velocity and a is uniform acceleration.
View SolutionThe distance travelled by a particle in nth second is Sn=u+a2(2n−1) where u is the velocity and a is the acceleration. The equation is
View SolutionFigure is a graph of the coordinate of a spider crawling along the x-axis. (a) Fraph tis velocity and acceleration as functionsof time. (b) In a motion diagram, show the position, velocity, and acceleration of the spider at the five times: t=2.5s, t=10 s, t=20 s, t=30 s,
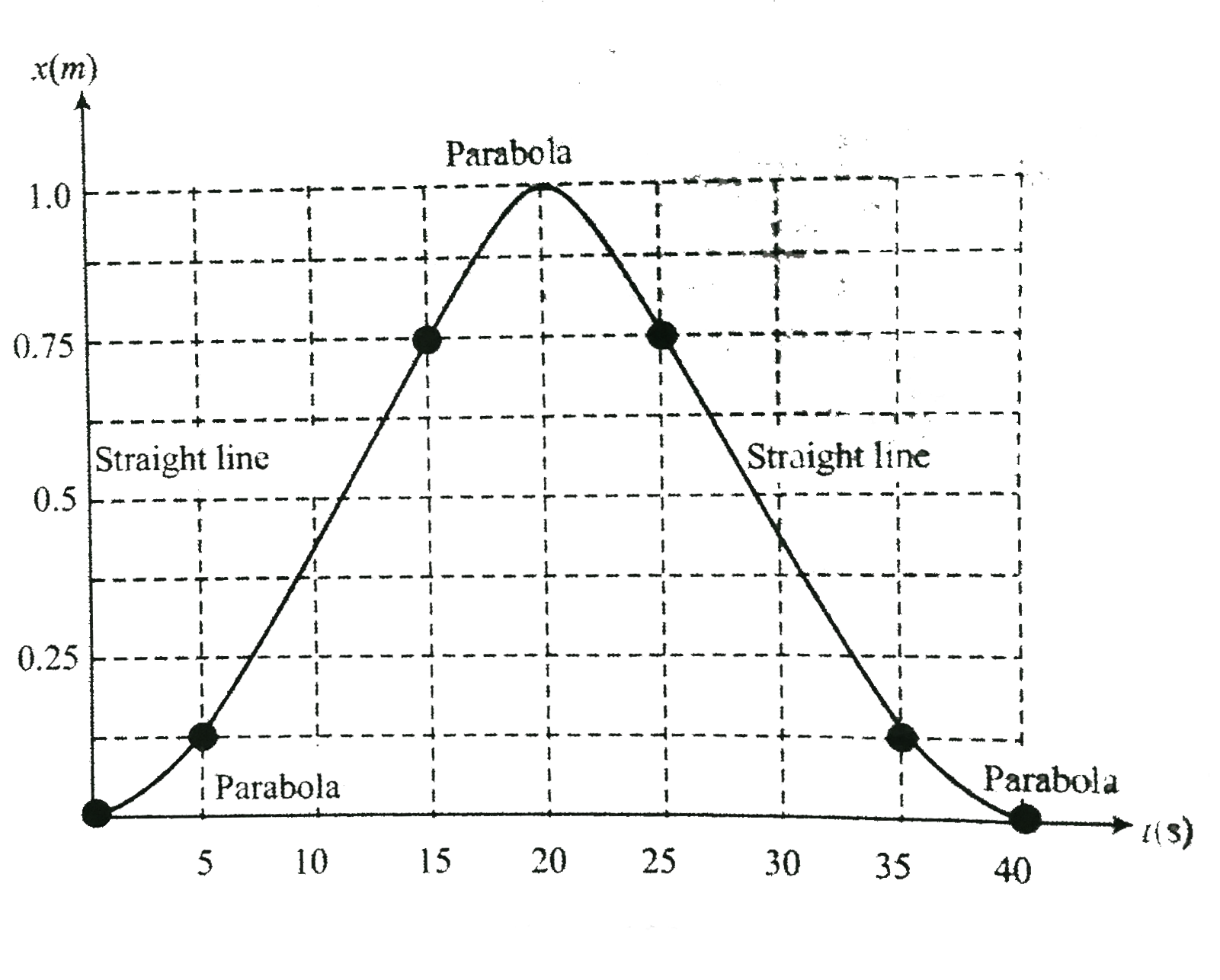 .
.
View SolutionA car is running on a straight road . The distance travelled and time taken are connected by the formula =t2−2t where t is measured in hours and s in km. When the odometer reading is 15, what is the speedometer reading ? [ Odometer measures s and the speedmeter measures velocity]
View Solution

