What is the significance of resistance ratio, ρ300K/ρ4.2K ?
To understand the significance of the resistance ratio ρ300Kρ4.2K, we can break down the concept into a few key steps:
Step 1: Define Resistance Ratio
The resistance ratio is defined as the ratio of the electrical resistivity of a metal at room temperature (approximately 300 K) to its resistivity at a much lower temperature (4.2 K, which is the temperature of liquid helium). Mathematically, it is expressed as:
Resistance Ratio=ρ300Kρ4.2K
Step 2: Understand Resistivity and Temperature Dependence
Resistivity (ρ) is a measure of how strongly a material opposes the flow of electric current. For metals, resistivity typically decreases as temperature decreases. This is due to reduced lattice vibrations and fewer phonon interactions at lower temperatures, allowing electrons to move more freely.
Step 3: Significance of the Resistance Ratio
The resistance ratio provides insight into the purity of the metal:
- A low resistance ratio (close to 1) indicates that the metal is highly pure, as the resistivity at low temperatures is significantly lower than at room temperature.
- A high resistance ratio suggests the presence of impurities or defects in the metal, which scatter electrons and increase resistivity at low temperatures.
Step 4: Application in Material Science
The resistance ratio is often used in material science and condensed matter physics to assess the quality of metals and their suitability for various applications, especially in superconductivity and electronic devices.
Final Answer
In summary, the significance of the resistance ratio ρ300Kρ4.2K lies in its ability to measure the purity of metals. A lower ratio indicates higher purity, while a higher ratio suggests the presence of impurities.
---
The resistance ratio is defined as the ratio of the electrical resistivity of a metal at room temperature (approximately 300 K) to its resistivity at a much lower temperature (4.2 K, which is the temperature of liquid helium). Mathematically, it is expressed as:
Resistance Ratio=ρ300Kρ4.2K
Resistivity (ρ) is a measure of how strongly a material opposes the flow of electric current. For metals, resistivity typically decreases as temperature decreases. This is due to reduced lattice vibrations and fewer phonon interactions at lower temperatures, allowing electrons to move more freely.
The resistance ratio provides insight into the purity of the metal:
- A low resistance ratio (close to 1) indicates that the metal is highly pure, as the resistivity at low temperatures is significantly lower than at room temperature.
- A high resistance ratio suggests the presence of impurities or defects in the metal, which scatter electrons and increase resistivity at low temperatures.
The resistance ratio is often used in material science and condensed matter physics to assess the quality of metals and their suitability for various applications, especially in superconductivity and electronic devices.
In summary, the significance of the resistance ratio ρ300Kρ4.2K lies in its ability to measure the purity of metals. A lower ratio indicates higher purity, while a higher ratio suggests the presence of impurities.
Similar Questions
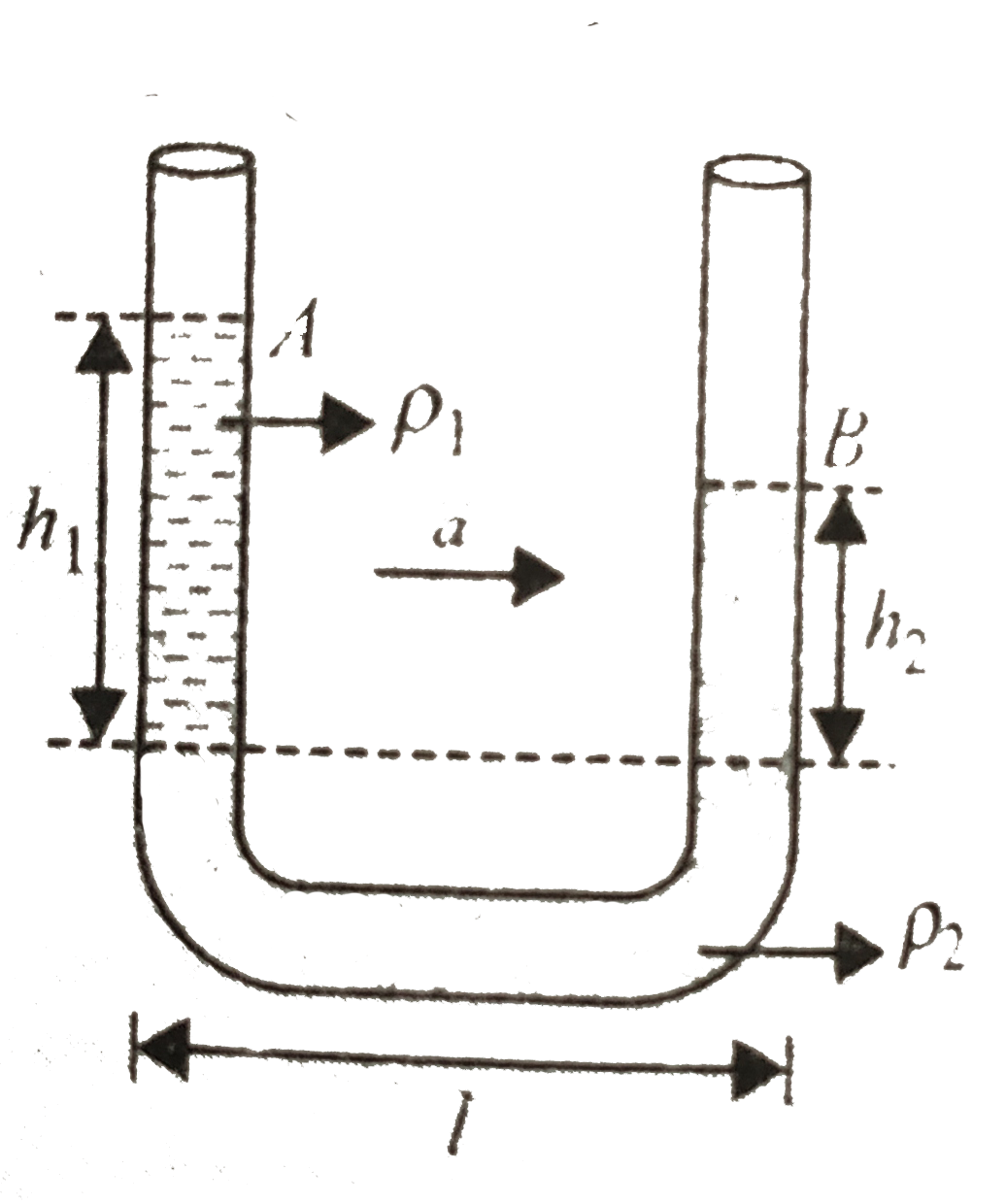
A U- tube shown in Fig. containing two liquids of specific gravities ρ1 and ρ2 is given an acceleration a in the horizontal direction. What is the ratio ρ1:ρ2?
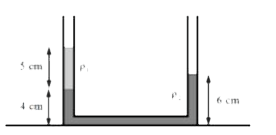
View SolutionA narrow U-tube placed on a horizontal surface contains two liquids of densities ρ1 and ρ2 . The columns of the liquids are indicated in the figure. The ratio ρ1ρ2 is equal to :
View Solution
Knowledge Check
The density of the core a planet is ρ1 and that of the outer shell is ρ2. The radii of the core and that of the planet are R and 2R respectively. The acceleration due to gravity at the surface of the planet is same as at a depth R. Find the ratio of ρ1ρ2
 A2.3B4.5C3.2D5.4
A2.3B4.5C3.2D5.4
Two wires of the same dimensions but resistivities ρ1 and ρ2 are connected in series. The equivalent resistivity of the combination is
View SolutionFig shows the same block of wood floating in three different liquids A,B and C of densities ρ1,ρ2 and ρ3 respectively. Which liquid has the highest density? Give reason for your answer.

View Solutionv1andv2 are the velocities of sound at the same temperature in two monoatomic gases of densities ρ1andρ2 respectively. If ρ1ρ2=14 then the ratio of velocities v1andv2 is
View SolutionThe density of the core a planet is ρ1 and that of the outer shell is ρ2. The radii of the core and that of the planet are R and 2R respectively. The acceleration due to gravity at the surface of the planet is same as at a depth R. Find the ratio of ρ1ρ2

View SolutionA closed organ pipe of length L and an open organ pipe contain gasses of densities ρ1 and ρ2, respectively. The compressibility of gasses are equal in both the pipes. Both the pipes are vibrating in their first overtone with same frequency . The length of the open organ pipe is
(a) L3
4l3
(c ) 4l3√ρ1ρ2
(d) 4l3√ρ2ρ1
View Solution
A jar filled with two non-mixing liquid 1 and 2 having densities ρ1 and ρ2 respectively. A solid ball, made of a material of density ρ3 is dropped in the jar. It come to equilibrium in the position shown in the figure. Which of the following is true for ρ1,ρ2 and ρ3?
View SolutionThree different liquids are filled in a U-tube as shown in figure. Their densities are ρ1,ρ2 and ρ3 respectively. From the figure we may conclude that
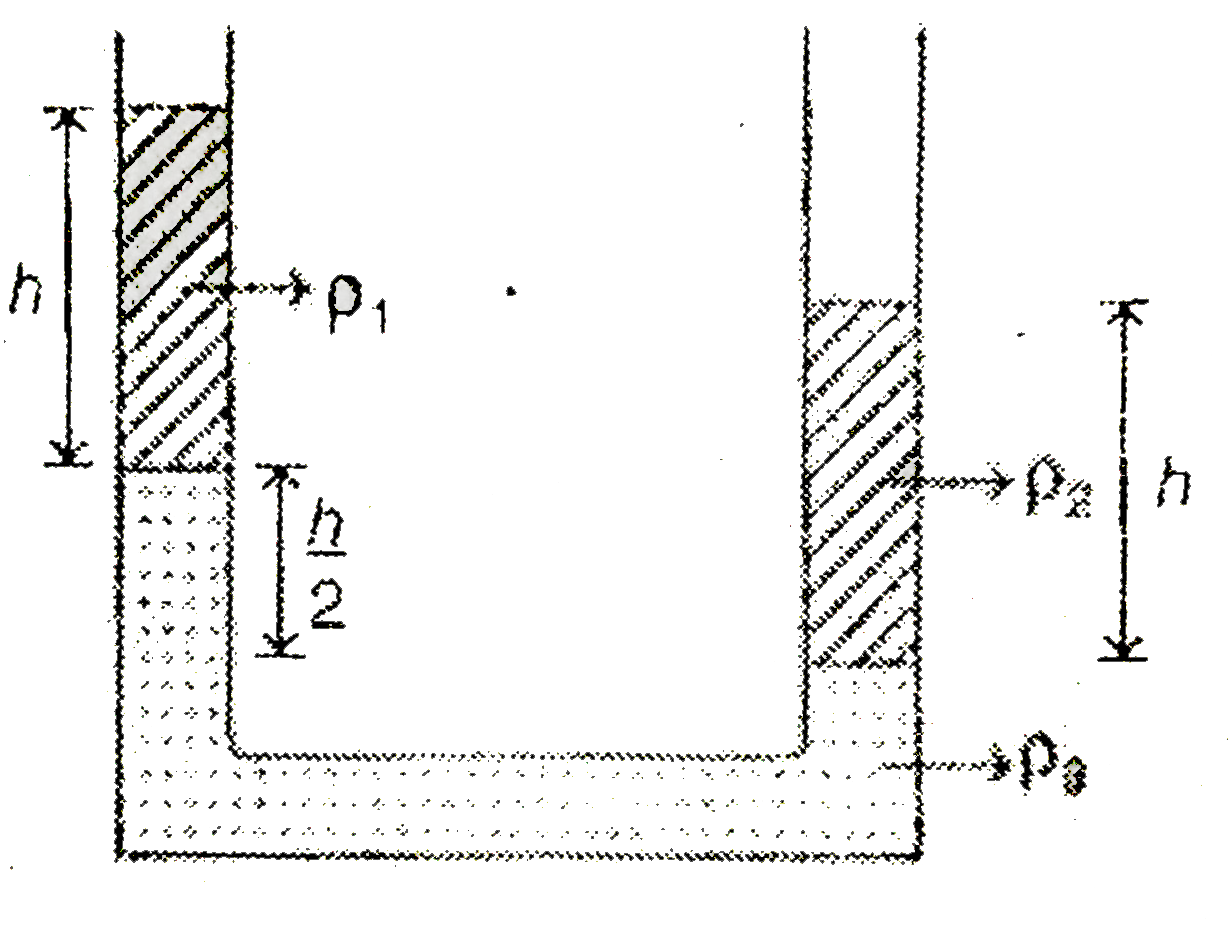
View Solution

