Assertion (A) : The vectors which can undergo parallel displacement without changing its magnitude and direction are called free vectors.
Reason (R ) : →a.→b=→b.→a
Both A and R are true and R is NOT the correct explanation of A
Both A and R are true but R is NOT the correct explanation of A
A is true but R is false
A is false but R is True
The correct Answer is:B
To solve the question, we need to analyze both the assertion (A) and the reason (R) given in the problem.
Step 1: Analyze the Assertion (A)
The assertion states: "The vectors which can undergo parallel displacement without changing its magnitude and direction are called free vectors."
- Definition of Free Vectors: A free vector is indeed defined as a vector that can be moved parallel to itself without altering its magnitude or direction. This means that the position of the vector does not affect its properties.
Step 2: Analyze the Reason (R)
The reason states: "vec(a) . vec(b) = vec(b) . vec(a)"
- Dot Product Property: This statement refers to the commutative property of the dot product of vectors. The dot product of two vectors is indeed commutative, meaning that the order of the vectors does not affect the result of the dot product.
Step 3: Determine the Relationship Between A and R
Now we need to determine if the reason (R) provides a valid explanation for the assertion (A).
- Explanation Check: While both the assertion and the reason are correct, the reason does not explain the assertion. The assertion is about the definition of free vectors, while the reason is a property of the dot product. There is no direct connection between the two statements.
Conclusion
Based on the analysis:
- Assertion (A) is true.
- Reason (R) is true.
- However, Reason (R) does not explain Assertion (A).
Thus, the correct option would be that both A and R are true, but R is not a correct explanation of A.
Final Answer
- Assertion (A) is true.
- Reason (R) is true.
- R does not explain A.
The assertion states: "The vectors which can undergo parallel displacement without changing its magnitude and direction are called free vectors."
The reason states: "vec(a) . vec(b) = vec(b) . vec(a)"
Now we need to determine if the reason (R) provides a valid explanation for the assertion (A).
Based on the analysis:
- Assertion (A) is true.
- Reason (R) is true.
- However, Reason (R) does not explain Assertion (A).
- Assertion (A) is true.
- Reason (R) is true.
- R does not explain A.
Similar Questions
Knowledge Check
- Question 1 - Select One
If for two vectors →A and →B,→A×→B=0, the vectors
AAre perpendicular to each otherBAre parallel to each otherCAct at an angle of 60∘DAct at an angle of 30∘ - Question 2 - Select One
Answer the following :
(i) Can 2 similar vectors of different magnitude yield a zero resultant? Can 3 yield?
(ii) Can →a+→b=→a−→b?
(iii) If →a+→b=→c & |→a|+∣∣→b∣∣=|→c|. What further information you can have about these vectors.
(iv) If →a & →b are two non zero vectors such that ∣∣→a+→b∣∣=∣∣→a+→b∣∣, then what is the angle between →a & →b.
(v) Time has a magnitude & direction. Is it a vector?
(iv) When will →a×→b=→a.→b?
(vii) Does the unit vectors →i,→j & →k have units?A→A×→B=→0BAB=12C→A,→B=48DA=5 - Question 3 - Select One
If →aand→b are two unit vectors, then the vector (→a+→b)×(→a×→b) is parallel to
A(ˆa−ˆb)B(ˆa+ˆb)C(2ˆa−ˆb)D(2ˆa+ˆb)
The three vectors →A,→Band→C are repesented in magnitude and direction by −−−−−−−→OP,−−→OQ, show that (S) is the mid point of (PQ).
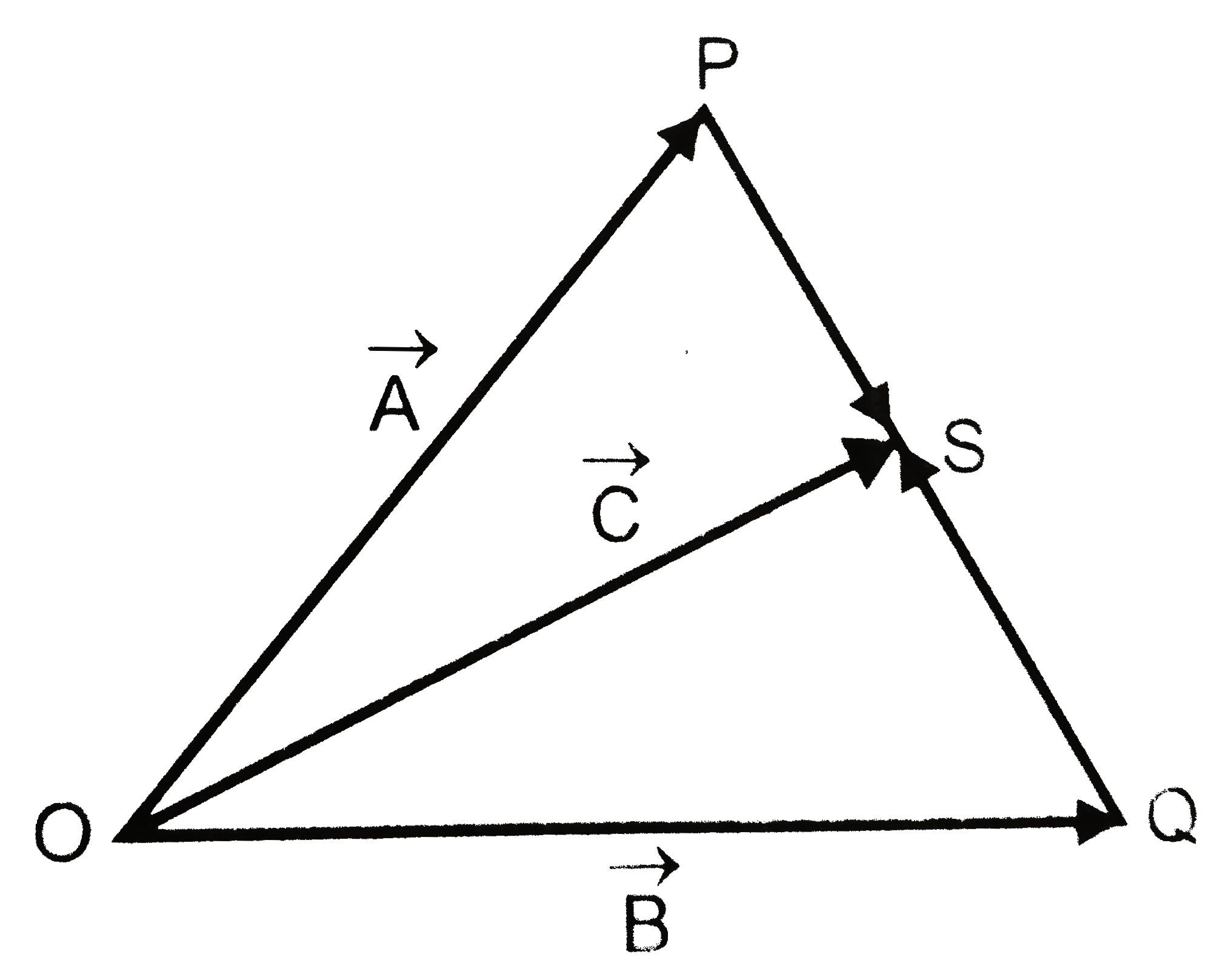 . View Solution
. View SolutionLet →a,→b,→c be three vectors mutually perpendicular to each other and have same magnitude. If a vector →r satisfies
→a×{(→r−→b)×→a}+→b×{(→r−→c)×→b}+→c×{(→r−→a)×→c}=→0, then →r is equal to :View SolutionIf →a,→b,and→c are mutually perpendicular vectors of equal magnitudes, then find the angle between vectors →aand→a+→b+→⋅
View SolutionIf →a and →b are vectors of equal magnitude, write the value of (→a+→b).→a−→b.
View SolutionIf →a,→b,→с are vectors such that →a.→b=0and→a+→b=→c, then
View Solution
