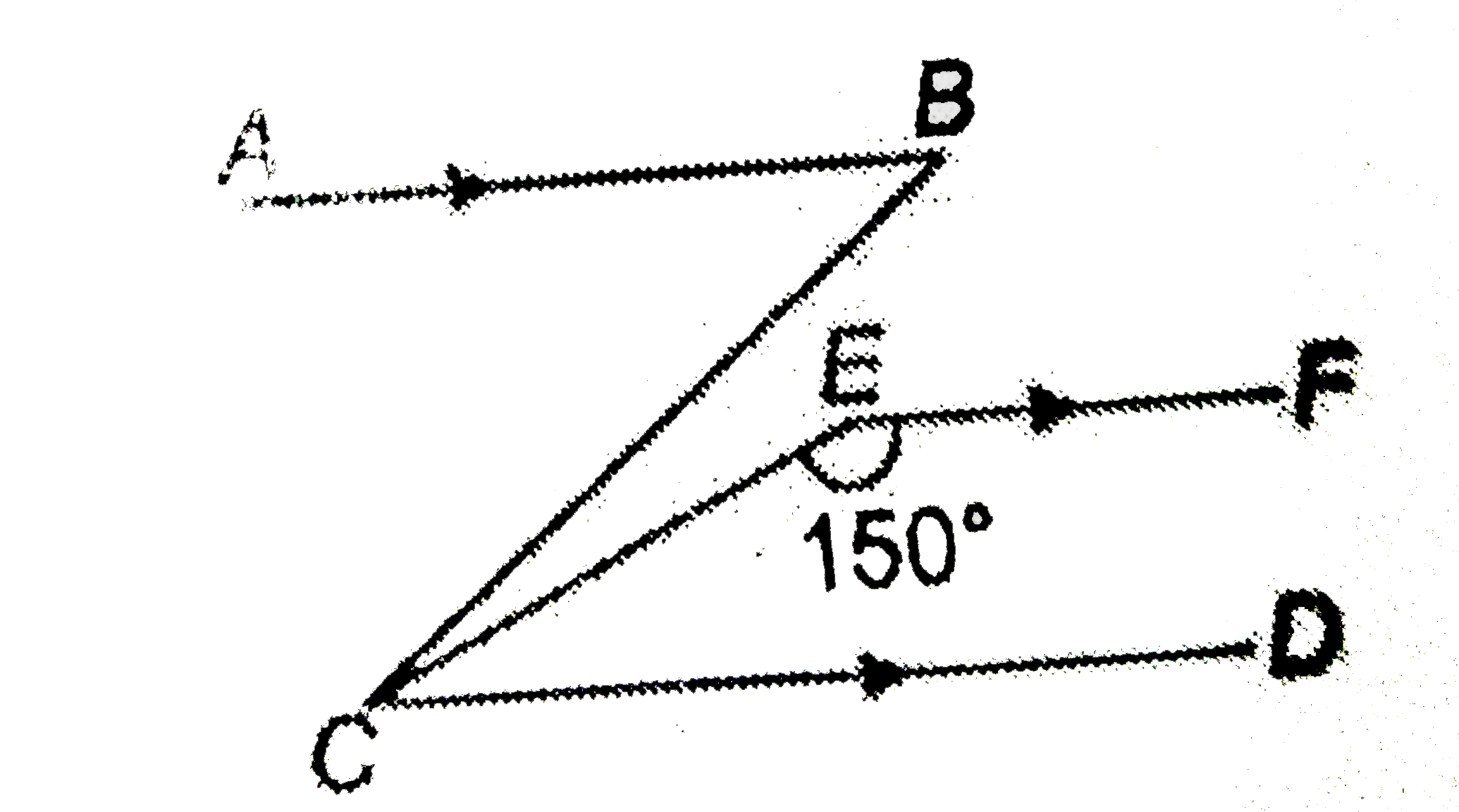
AB and CD are two parallel lines. PQ cuts AB and CD at E and F respectively. EL is the bisector of ∠BEF. If ∠LEB=35∘ ,then ∠CFQ will be :
130∘
85∘
110∘
95∘
The correct Answer is:C
Step by step video, text & image solution for AB and CD are two parallel lines. PQ cuts AB and CD at E and F respectively. EL is the bisector of angle BEF. If angle LEB=35^@ ,then angle CFQ will be : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
- BOOK - BHARDWAJ ACADEMYCHAPTER - GEOMETRYEXERCISE - Chapter Exercise (Pervious Years Questions)25videos
GEOMETRY
- BOOK - BHARDWAJ ACADEMYCHAPTER - GEOMETRYEXERCISE - Chapter Exercise (Pervious Years Questions)25videos
GEOMETRY
- BOOK - BHARDWAJ ACADEMYCHAPTER - EVALUATION EXERCISE - CHAPTER EXERCISE (Previous Years. Questions)19videos
EVALUATION
- BOOK - BHARDWAJ ACADEMYCHAPTER - LCM AND HCF EXERCISE - CHAPTER EXERCISE35videos
LCM AND HCF
Similar Questions
Knowledge Check
- Question 1 - Select One
AB and CD are two parallel lines, PQ cuts AB and CD at E and F respectively. EL is the bisector of ∠BEF. If ∠LEB=35∘ then ∠CFQ will be :
A70∘B55∘C110∘D125∘ - Question 2 - Select One
AB and CD are two parallel lines and a transversal PO intersects AB and CD at M and N respectively. The bisector of the interior angles form a quadrilateral :
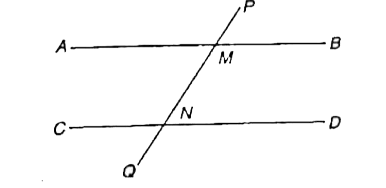 ArectangleBsquareCparallelogramDnone of these
ArectangleBsquareCparallelogramDnone of these - Question 3 - Select One
Two parallel lines AB and CD are intersected by a transversal EF at M and N respectively.
The lines MP and NP are the bisectors of interior angles ∠BMN and ∠DNM on the same side of the transversal. Then ∠MPN is equal to :A60∘B90∘C45∘D120∘
In the given figure, AB∣∣CD and a transversal t cuts them at E and F respectively. If EP and FQ are the bisectors of ∠AEF and ∠EFD respectively, prove that EP∣∣FQ.
 View Solution
View SolutionIn the given figure, AB∣∣CD and a transversal t cuts them at E and F respectively. If EG and FG are this bisectors of ∠BEF and ∠EFD respectivelym prove that ∠EGF=90∘.
 View Solution
View SolutionAB and CD are parallel straight lines. EG intersects the lines AB and CD at F and G respectively. If ∠AFE=60∘ and the straight line HI bisects ∠EGD, then ∠DGI is
View SolutionAB and CD are two parallel lines. The points B and C are joined such that <ABC=65∘. A line CE is drawn making angle of 35∘ with the line CB, EF is drawn parallel to AB, as shown in figure, then <CEF is
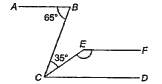 View Solution
View SolutionTwo parallel lines AB and CD are intersected by a transversal EF at M and N respectively.
The lines MP and NP are the bisectors of interior angles ∠BMN and ∠DNM on the same side of the transversal. Then ∠MPN is equal to :View Solution