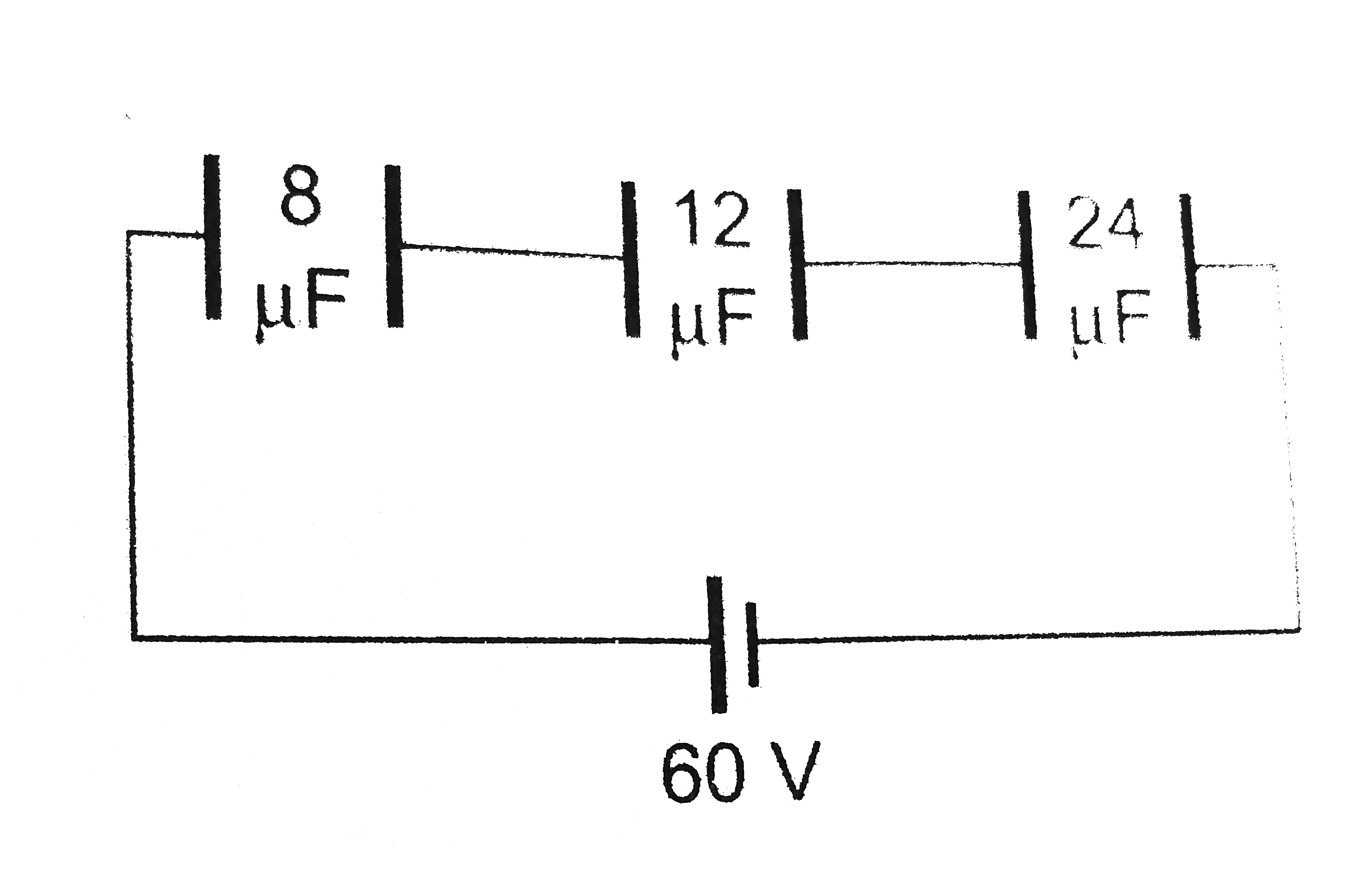
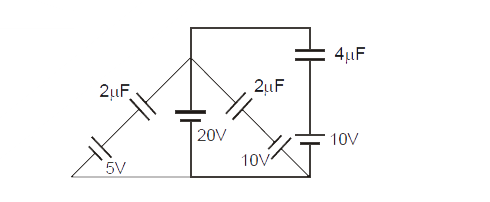
If three capacitors are connected in a parallel capacitor network then, Choose the correct statements out of the following:
(l) Potential difference across each capacitor is same.
(II) For each capacitor, charges is different
(III) Voltage applied is different for each capacitor.
(IV)For each capacitor, charges are same.
(II) and (III)
(l) and (II)
(l) and (III)
(III) and (IV)
The correct Answer is:B
To solve the problem regarding the characteristics of capacitors connected in a parallel network, we will analyze each statement one by one.
1. Understanding Capacitors in Parallel:
- When capacitors are connected in parallel, they share the same voltage across their terminals. This is a fundamental property of parallel circuits.
2. Analyzing Statement (I):
- Statement (I): "Potential difference across each capacitor is same."
- Since all capacitors in a parallel configuration are connected directly across the same voltage source, this statement is correct.
3. Analyzing Statement (II):
- Statement (II): "For each capacitor, charge is different."
- The charge on each capacitor can be calculated using the formula Q=C×V, where C is the capacitance and V is the voltage. Since the voltage V is the same for all capacitors but the capacitances C1,C2,C3 can be different, the charges Q1,Q2,Q3 will also be different. Thus, this statement is correct.
4. Analyzing Statement (III):
- Statement (III): "Voltage applied is different for each capacitor."
- This statement is incorrect because, in a parallel configuration, the voltage across each capacitor is the same, as established in Statement (I).
5. Analyzing Statement (IV):
- Statement (IV): "For each capacitor, charges are same."
- This statement is also incorrect because, as mentioned earlier, the charges on each capacitor depend on their capacitance and the common voltage. If the capacitances are different, the charges will also be different.
Conclusion
From the analysis:
- Correct Statements: (I) and (II)
- Incorrect Statements: (III) and (IV)
Thus, the correct answer is that statements (I) and (II) are true.
- When capacitors are connected in parallel, they share the same voltage across their terminals. This is a fundamental property of parallel circuits.
- Statement (I): "Potential difference across each capacitor is same."
- Since all capacitors in a parallel configuration are connected directly across the same voltage source, this statement is correct.
- Statement (II): "For each capacitor, charge is different."
- The charge on each capacitor can be calculated using the formula Q=C×V, where C is the capacitance and V is the voltage. Since the voltage V is the same for all capacitors but the capacitances C1,C2,C3 can be different, the charges Q1,Q2,Q3 will also be different. Thus, this statement is correct.
- Statement (III): "Voltage applied is different for each capacitor."
- This statement is incorrect because, in a parallel configuration, the voltage across each capacitor is the same, as established in Statement (I).
- Statement (IV): "For each capacitor, charges are same."
- This statement is also incorrect because, as mentioned earlier, the charges on each capacitor depend on their capacitance and the common voltage. If the capacitances are different, the charges will also be different.
From the analysis:
- Correct Statements: (I) and (II)
- Incorrect Statements: (III) and (IV)
Topper's Solved these Questions
- SAMPLE PAPER 7BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - SECTION-C
6 Videos
- SAMPLE PAPER 7BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - SECTION-C
6 Videos
- SAMPLE PAPER 6BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section-C
6 Videos
- SAMPLE PAPER 9 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 9 EXERCISE - SECTION - C
3 Videos
Similar Questions
Knowledge Check
Find charges on different capacitors.
 A30μC 20μC 10μCB300μC 200μC 100μCC30μC 10μC 10μCD10μC 20μC 10μC
A30μC 20μC 10μCB300μC 200μC 100μCC30μC 10μC 10μCD10μC 20μC 10μC
Find charge on each capacitor.
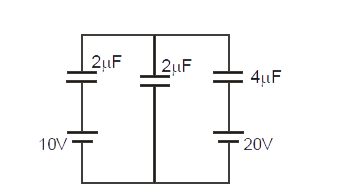
View SolutionFind charge on each capacitor

View SolutionFind charge on each capacitor and potential difference across each capacitor .

View SolutionThree uncharged capacitors are connected in the circuit as shown. What should be the value of C3(in uF) so that potential difference across each capacitor is same
View SolutionFind charge in each capacitor:
View SolutionFind charge in each capacitor:
View SolutionWhen a number of capacitor are connected in series, ……….. Each capacitor .
View Solution