A metallic rod of length L rotates at an angular speed ω, normal to a uniform magnetic field. If the resitance of rod is R the heat dissipated is:
14B2L4ω2tR
12B2L2ωtR
14B2L2ω2t2R
14BL2ω4tR
The correct Answer is:A
To solve the problem, we need to find the heat dissipated in a metallic rod of length L rotating with an angular speed ω in a uniform magnetic field B with resistance R.
1. Understanding the Setup:
- We have a metallic rod of length L rotating about an axis with angular speed ω.
- The rod is placed in a uniform magnetic field B, which is perpendicular to the plane of rotation.
2. Induced EMF Calculation:
- The induced electromotive force (EMF) in the rod can be calculated using the formula:
E=B⋅v⋅L
- Here, v is the linear velocity of a point at a distance x from the axis of rotation, given by:
v=ω⋅x
- Therefore, the induced EMF for a small segment dx of the rod at distance x is:
dE=B⋅(ω⋅x)⋅dx
3. Total Induced EMF:
- To find the total induced EMF E in the entire rod, we integrate dE from 0 to L:
E=∫L0B⋅(ω⋅x)dx=Bω∫L0xdx
- The integral of x from 0 to L is:
∫L0xdx=L22
- Thus, the total induced EMF is:
E=Bω⋅L22=BωL22
4. Current Calculation:
- Using Ohm's law, the current I flowing through the rod can be calculated as:
I=ER=BωL22R=BωL22R
5. Heat Dissipated:
- The heat Q dissipated in the rod over a time T can be calculated using the formula:
Q=I2RT
- Substituting for I:
Q=(BωL22R)2RT
- Simplifying this expression:
Q=B2ω2L44R2RT=B2ω2L4T4R
Final Answer:
The heat dissipated in the rod is:
Q=B2ω2L4T4R
- We have a metallic rod of length L rotating about an axis with angular speed ω.
- The rod is placed in a uniform magnetic field B, which is perpendicular to the plane of rotation.
- The induced electromotive force (EMF) in the rod can be calculated using the formula:
E=B⋅v⋅L
- Here, v is the linear velocity of a point at a distance x from the axis of rotation, given by:
v=ω⋅x
- Therefore, the induced EMF for a small segment dx of the rod at distance x is:
dE=B⋅(ω⋅x)⋅dx
- To find the total induced EMF E in the entire rod, we integrate dE from 0 to L:
E=∫L0B⋅(ω⋅x)dx=Bω∫L0xdx
- The integral of x from 0 to L is:
∫L0xdx=L22
- Thus, the total induced EMF is:
E=Bω⋅L22=BωL22
- Using Ohm's law, the current I flowing through the rod can be calculated as:
I=ER=BωL22R=BωL22R
- The heat Q dissipated in the rod over a time T can be calculated using the formula:
Q=I2RT
- Substituting for I:
Q=(BωL22R)2RT
- Simplifying this expression:
Q=B2ω2L44R2RT=B2ω2L4T4R
The heat dissipated in the rod is:
Q=B2ω2L4T4R
Topper's Solved these Questions
- SAMPLE PAPER 7Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 7Exercise:SECTION-C
Explore 6 Videos
- SAMPLE PAPER 7Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 7Exercise:SECTION-C
Explore 6 Videos
- SAMPLE PAPER 6Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 6Exercise:Section-C
Explore 6 Videos
- SAMPLE PAPER 9 Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 9 Exercise:SECTION - C
Explore 3 Videos
Similar Questions
A metallic rod of length l is rotated at a constant angular speed ω, normal to a uniform magnetic field B. Derive an expression for the current induced in the rod, if the resistance of the rod is R.
View SolutionA copper rod of length L rotates with an angular with an angular speed 'ω' in a uniform magnetic field B. find the emf developed between the two ends of the rod. The field in perpendicular to the motion of the rod.
View Solution
Knowledge Check
A copper rod of length L rotates with an angular with an angular speed 'ω' in a uniform magnetic field B. find the emf developed between the two ends of the rod. The field in perpendicular to the motion of the rod.
ABωl2B12Bωl2C2Bωl2D14Bωl2A rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the rod is
ABl2ω2BzeroC(Bl2ω8)D2Bl2ωA conducting rod of length 2l is rotating with constant angular speed ω about is perpendicular bisector. A uniform magnetic field →B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is
 A12Bωl2B18Bωl2CZeroDBωl2
A12Bωl2B18Bωl2CZeroDBωl2
(a) A metal rod of length L rotates about an end with a uniform angular velocity ω . A uniform magnetic field B exists in the direction of the axis of rotation. Calculate the emf induced between the ends of the rod. Neglect the centripetal force acting on the free electrons as they move in circular paths.
(b) A rod of length L rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. Find the potential difference (i) between the centre of rod and one end and (ii) between the two ends of the rod.
View SolutionA copper rod of length l rotates an angular velocity ω in a uniform magnetic field B as show in figure . What is the induced emf across its ends ?
View SolutionA metal rod length l rotates about on end with a uniform angular velocity ω. A uniform magnetic field →B exists in the direction of the axis of rotation. Calculate the emf induced between the ends of the rod. Neglect the centripetal force acting on the free electrons as they money in circular paths.
View SolutionA conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?

View SolutionA conducting wheel in which there are four rods of length l is rotating with angular velocity ω in a uniform magnetic field B . The induced potential difference between its centre and rim will be __
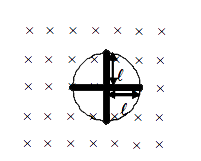
View Solution

