The radius of spherical capacitor when capacitance is 1 μF is:
1.11m
9km
10m
1.11cm
The correct Answer is:B
To find the radius of a spherical capacitor when the capacitance is given as 1 microfarad (1 µF), we can use the formula for the capacitance of a spherical capacitor. The capacitance C of a spherical capacitor is given by:
C=4πϵ0R1R2R2−R1
For a spherical capacitor with an inner radius R1 and an outer radius R2, if we assume R1 is negligible compared to R2 (which is a common assumption for large capacitors), we can simplify the formula to:
C≈4πϵ0R
where R is the radius of the outer sphere, and ϵ0 (the permittivity of free space) is approximately 8.85×10−12F/m.
Given that the capacitance C=1μF=1×10−6F, we can rearrange the formula to find R:
R=C4πϵ0
Substituting the values:
R=1×10−64π×8.85×10−12
Calculating the denominator:
4π×8.85×10−12≈1.112×10−10
Now substituting this back into our equation for R:
R=1×10−61.112×10−10≈8.99×103m
Thus, the radius R is approximately 8.99km.
Final Answer:
The radius of the spherical capacitor when the capacitance is 1 µF is approximately 9 km.
---
The radius of the spherical capacitor when the capacitance is 1 µF is approximately 9 km.
Topper's Solved these Questions
- SAMPLE PAPER 7BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - SECTION-B
24 Videos
- SAMPLE PAPER 7BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - SECTION-C
6 Videos
- SAMPLE PAPER 6BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section-C
6 Videos
- SAMPLE PAPER 9 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 9 EXERCISE - SECTION - C
3 Videos
Similar Questions
A circuit has section AB as shown in The emf of the cell is 10V, and the capacitors have capacitances C1=1μF and C2=2μF.
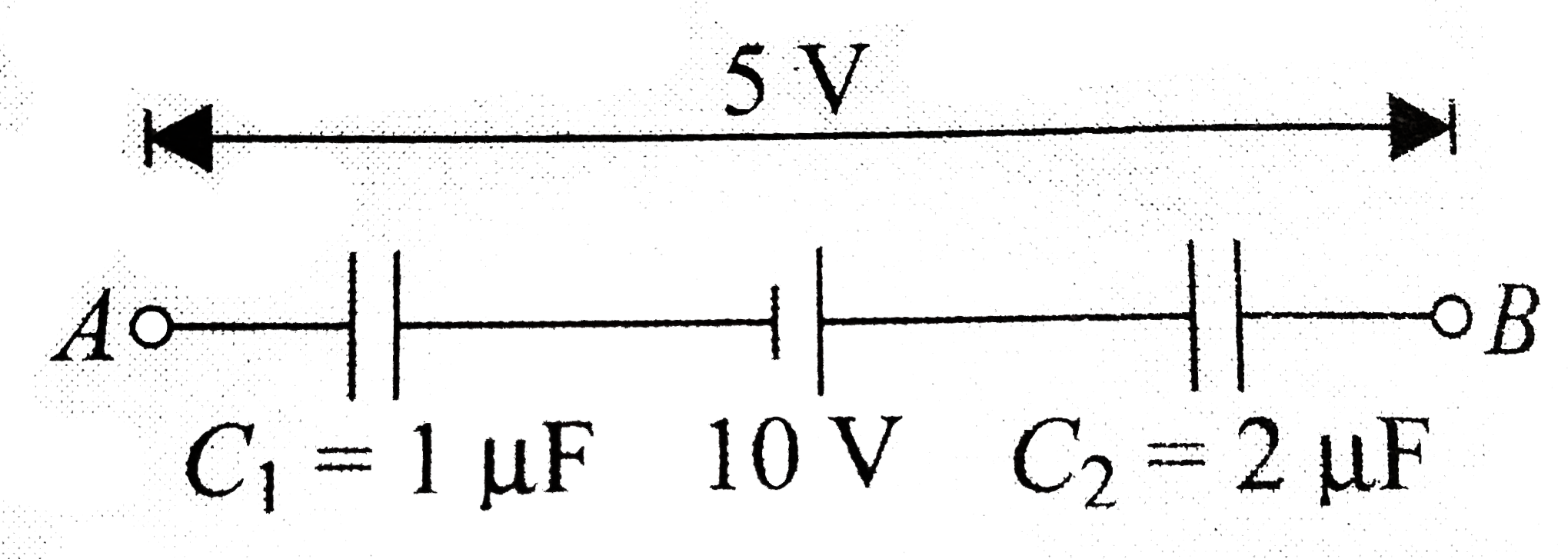 .
.
View SolutionHow many different values of capacitances can be obtained with the three given capacitors of capacitances 1μF,3μFand5μF? Use all the capacitors while forming any combination.
View Solution
Knowledge Check
An infinite number of identical capacitors each of capacitance 1μF are connected 1μF are connected as shown in Fig. Then the equivalent capacitance between A and B is
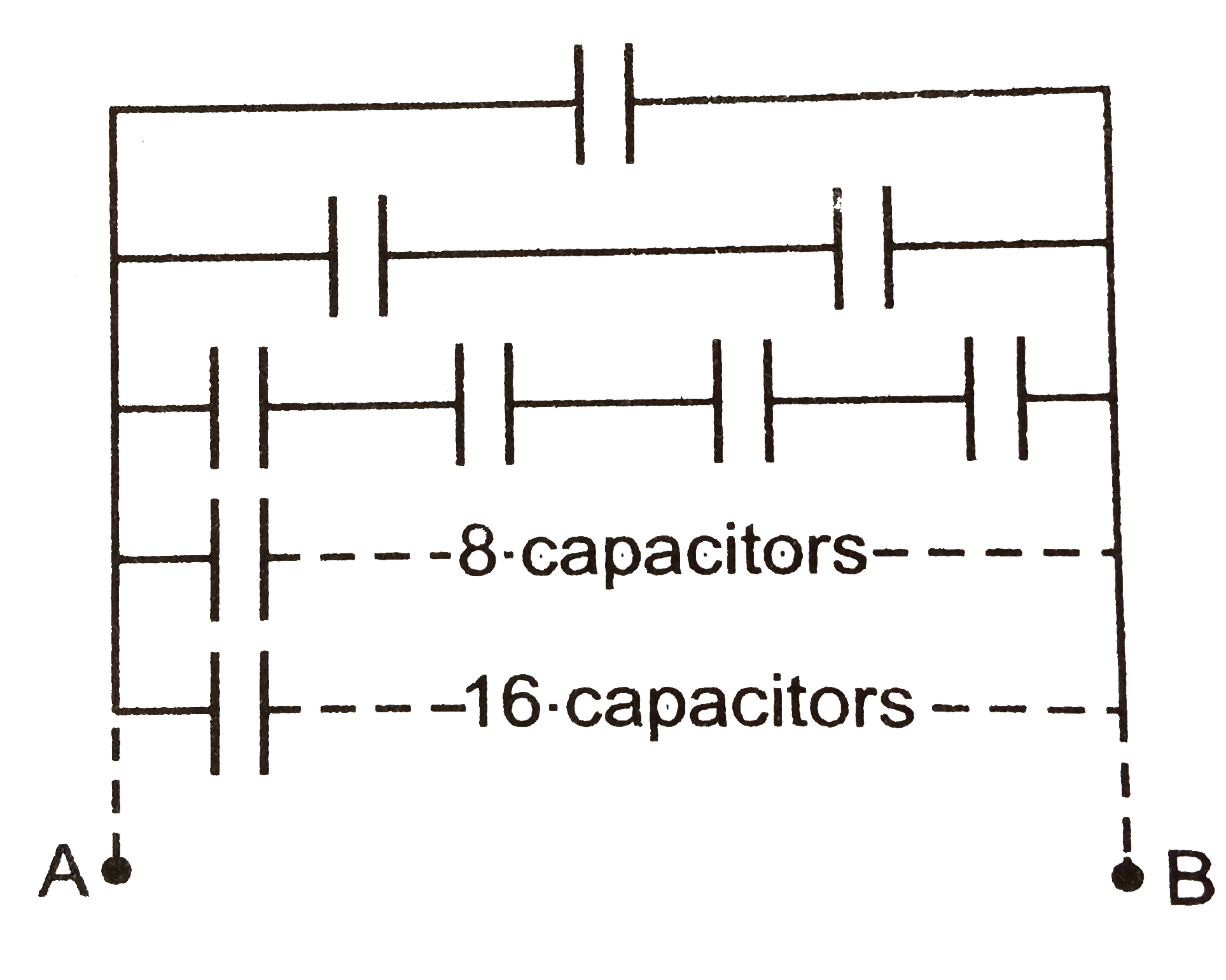 A1μFB2μFC12μFD∞
A1μFB2μFC12μFD∞Shows a part of a circuit. If all the capacitors have a capacitance of 2μF, then the
 . Acharge on C3 is zeroBcharge on C3 is 12μCCcharge on C1 is 6μCDcharge on C1 in 6μC
. Acharge on C3 is zeroBcharge on C3 is 12μCCcharge on C1 is 6μCDcharge on C1 in 6μCFind the energy stored in a capacitor of capacitance 100μF when it is charged to a potential difference of 20 V.
A0.02JB0.04JC0.01JD0.05J
In the shown network, find the charges on capacitors of capacitances 5μF and 3μF, in steady state.
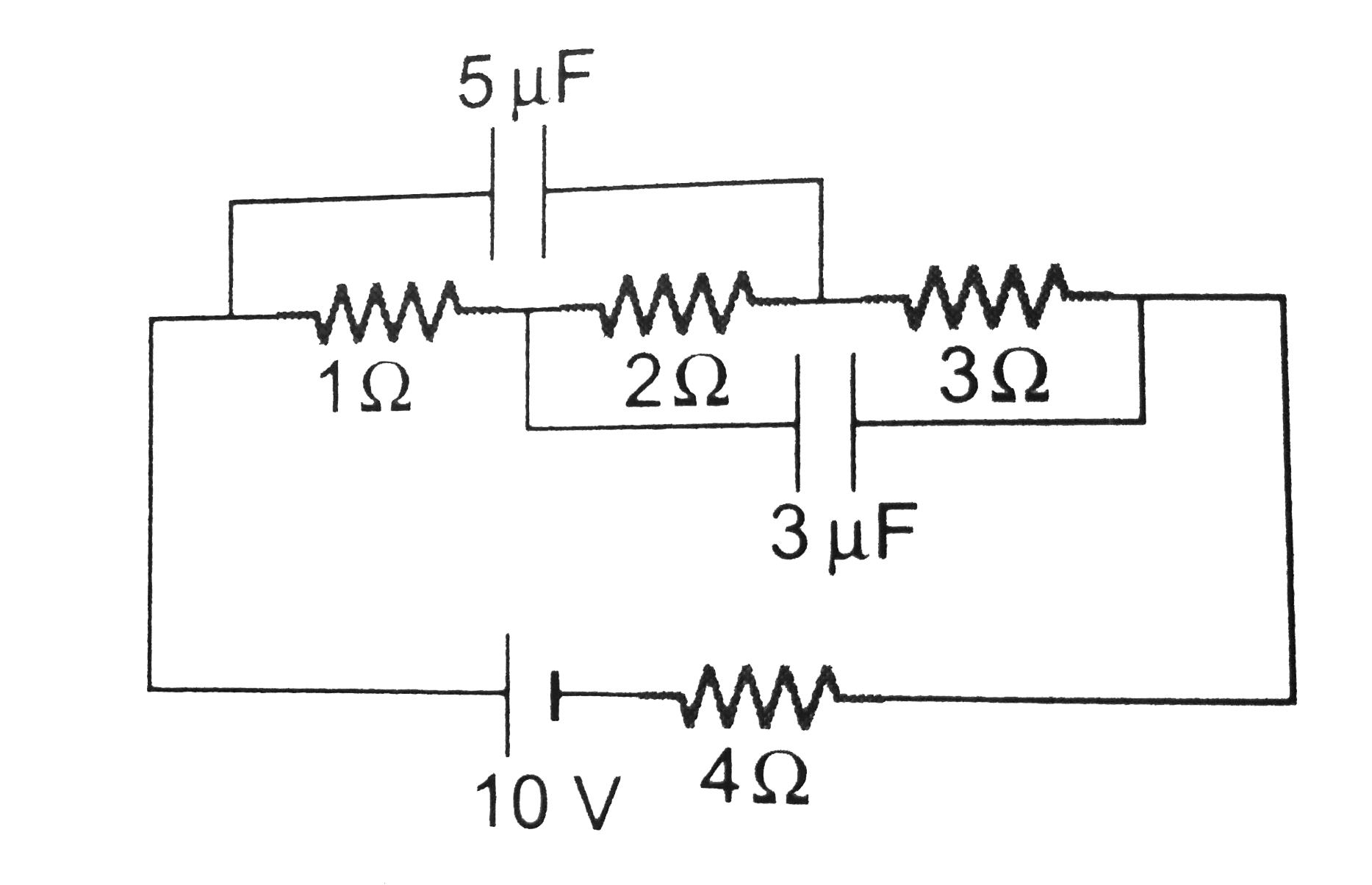
View SolutionFind the equivalent capacitance between terminals A & C, if each capacitor is of capacitance 4μF
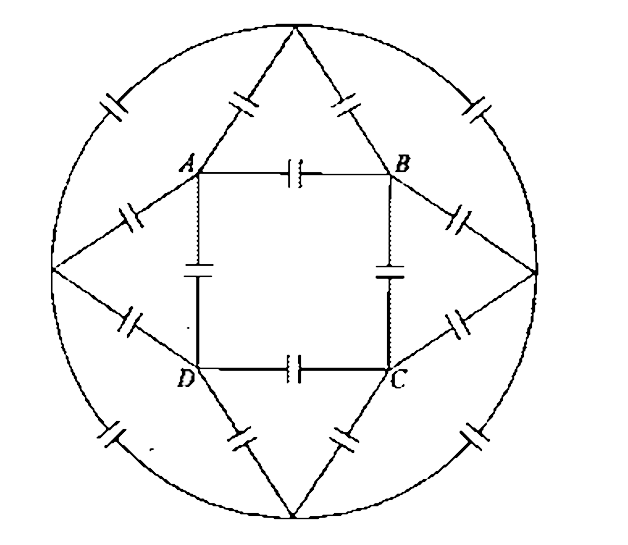
View SolutionAn infinite number of capacitors, having capacitances 1μF,2μF,4μFand8μF….. are connected in series. The equivalent capacitance of the system is
View SolutionIn the above question, if the initial capacitance of the capacitor was 2μF, the amount of heat produced when the dielectric is inserted.
View SolutionIn the circuit shown in figure, the charge stored on a capacitor of capacitance 3μF is
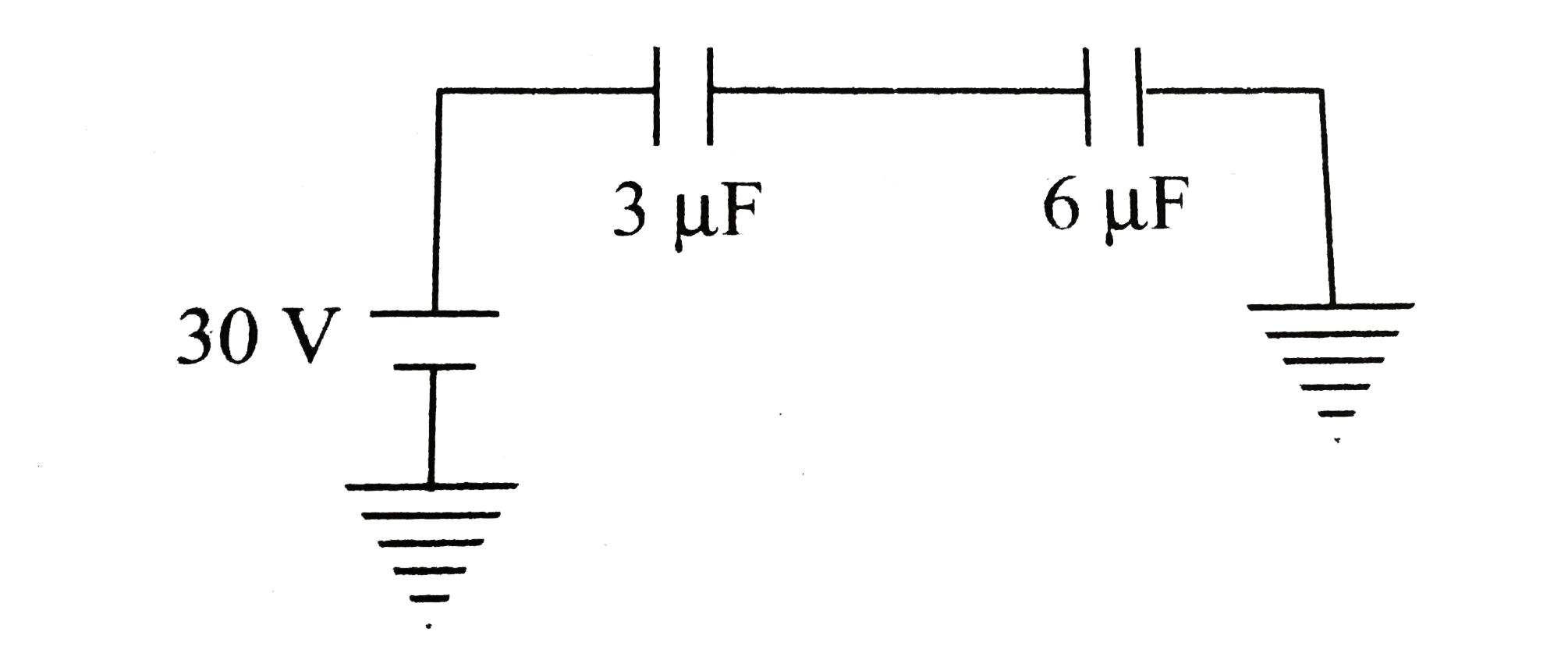
View Solution
