ε0=ε0sinωt, represents an ac equation. The time in which emf becomes half of its maximum value starting from zero is:
T2
T3
T6
T12
The correct Answer is:D
To solve the problem of finding the time at which the EMF becomes half of its maximum value in the AC equation E=E0sin(ωt), we can follow these steps:
Step 1: Identify the maximum value of EMF
The maximum value of EMF, denoted as Emax, is given by E0. Therefore, half of the maximum value is:
Ehalf=E02
Step 2: Set up the equation
We need to find the time t when the EMF equals half of its maximum value:
E0sin(ωt)=E02
Step 3: Simplify the equation
Dividing both sides by E0 (assuming E0≠0):
sin(ωt)=12
Step 4: Solve for ωt
The sine function equals 12 at specific angles. The principal angle is:
ωt=π6
However, sine is periodic, so it can also equal 12 at:
ωt=π6+nπ(n∈Z)
Step 5: Substitute ω
We know that ω=2πT, where T is the time period. Substituting this into our equation gives:
2πTt=π6
Step 6: Solve for t
Rearranging the equation to solve for t:
t=T12
Conclusion
Thus, the time in which the EMF becomes half of its maximum value starting from zero is:
t=T12
The maximum value of EMF, denoted as Emax, is given by E0. Therefore, half of the maximum value is:
Ehalf=E02
We need to find the time t when the EMF equals half of its maximum value:
E0sin(ωt)=E02
Dividing both sides by E0 (assuming E0≠0):
sin(ωt)=12
The sine function equals 12 at specific angles. The principal angle is:
ωt=π6
However, sine is periodic, so it can also equal 12 at:
ωt=π6+nπ(n∈Z)
We know that ω=2πT, where T is the time period. Substituting this into our equation gives:
2πTt=π6
Rearranging the equation to solve for t:
t=T12
Thus, the time in which the EMF becomes half of its maximum value starting from zero is:
t=T12
Topper's Solved these Questions
- SAMPLE PAPER 2BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 2EXERCISE - SECTION-B
24 Videos
- SAMPLE PAPER 2BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 2EXERCISE - SECTION-C
6 Videos
- SAMPLE PAPER 04 (SOLVED)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 04 (SOLVED)EXERCISE - SECTION-C
6 Videos
- SAMPLE PAPER 3BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 3EXERCISE - SECNTION -C
6 Videos
Similar Questions
Find the time required for a 60 Hz alternating current to reach its peak value starting from zero.
View SolutionA pure inductor coil having inductance L is connected to a resistance R and a cell of emf V0 as shown in the figure. Switch ‘S’ is closed at t = 0.
(a) Plot the variation of voltage across the resistance and the inductance as a function of time
(b) Find the time (t1) when the two curves, obtained in (a) intersect.
(c) A student decides to start counting time from the instant the current becomes half its maximum value. Show the graphical plot of current vs time as obtained by this student.
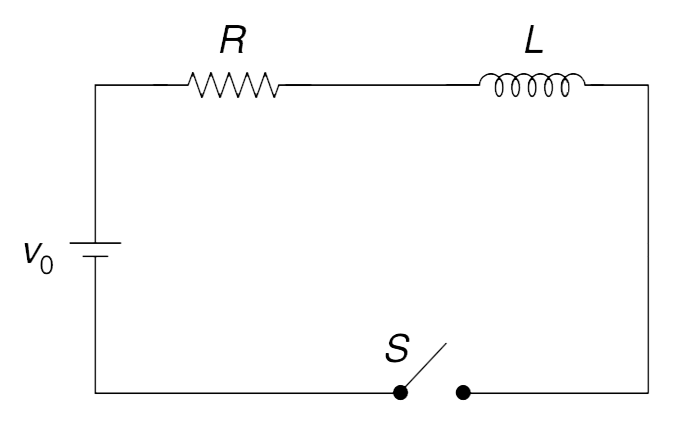
View Solution
Knowledge Check
An alternating e.m.f. is given by E=E0sinωt. In what time the e.m.f. will have half its maximu value, if E starts from zero?
AA. T4BB. T8CC. T12DD. T16The time taken by an AC of 50Hz in reaching from zero to its maximum value will be
A0.5sB0.005sC0.05sD5sA resistor of resistance R, capacitor of capacitance C and inductor of inductance L are connected in parallel to AC power source of voltage ε0 sin ωt. The maximum current through the resistance is half of the maximum current through the power source. Then value of R is
A√3∣∣ωC−1ωL∣∣B√3∣∣∣1ωC−ωL∣∣∣C√5∣∣∣1ωC−ωL∣∣∣DNone of these
Calculate the time taken by 60 Hz a.c source to reach its negative peak value from zero value ?
View SolutionFind the time taken by 60 Hz a.c. to reach its peak value from zero.
View SolutionThe electric current in an AC circuit is given by I=I0sinωt.What is the time taken by the current to change from its maximum value to the rms value?
View SolutionThe time taken by an alternating current i=i0sin(314t) in reaching from zero to its maximum value will be
View SolutionAn AC source is rated at 220V,50Hz. The time taken for voltage to change from its peak value to zero is
View Solution
