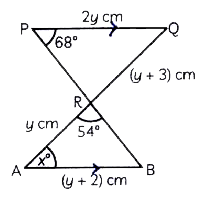
Given that △PQR is similar to △BAR, find the value of x:
The correct Answer is:58
Step by step video, text & image solution for Given that triangle PQR is similar to triangle BAR, find the value of x: by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBook:EDUCART PUBLICATIONChapter:TRIANGLESExercise:SHORT ANSWER (SA-II) TYPE QUESTIONS
Explore 21 Videos
- TRIANGLESBook:EDUCART PUBLICATIONChapter:TRIANGLESExercise:LONG ANSWER TYPE QUESTIONS
Explore 10 Videos
- TRIANGLESBook:EDUCART PUBLICATIONChapter:TRIANGLESExercise:VERY SHORT QUESTIONS
Explore 10 Videos
- SURFACE AREAS AND VOLUMESBook:EDUCART PUBLICATIONChapter:SURFACE AREAS AND VOLUMESExercise:LONG ANSWER TYPE QUESTIONS
Explore 30 Videos
Similar Questions
Knowledge Check
Triangle PQR is such that PQ= 9cm, QR= 6cm, PR 7.5cm and triangle PQR is similar to triangle XYZ. If XY= 18cm, find the value of YZ.
A. 15cm B. 18cm C. 12cm D. 9cmAABCCBDDI is the incentre of a triangle PQR and ∠=107∘ then find the value ∠P.
A56°B34°C26°D42°PQR is a triangle. S and T are the midpoints of the sides PQ and PR respectively. Which of the following is TRUE?
I. Triangle PST is similar to triangle PQR.
II. ST = 1/2(QR)
III. ST is parallel to QR. / ST, QRAOnly I and IIBOnly II and IIICOnly I and IIIDAll I, II and III
Tangent lines are drawn at the points P and Q where f''(x) vanishes for the function f(x)=cos x on [0,2π] The tangent lines at P and Q intersect each other at R so as to form a triangle PQR. If area triangle PQR is kπ2 then find the value of 36k.
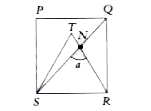
View SolutionIn the given below ,PQRS is a square and STR is an euilateral triangle . Find the value of a .
View SolutionIf triangle ABC is similar to triangle PQR , Perimeter of triangle ABC = 30 cm , Perimeter of triangle = 45 cm , PR = 9 cm then find AC.
View SolutionIn the given figure, PQR is a equilateral triangle and PS is the angle bisector of ∠P. What is the value of RT: RQ ?
View SolutionTriangle ABC is similar to triangle PQR and AB : PQ = 2 : 3. AD is the median to the side BC in triangle ABC and PS is the median to the side QR in triangle PQR. What is the value of (BD/QS)2?
View Solution