△ABC−△DEF such that DE=3cm,EF=2cm,DF=2.5cm and BC=4cm. Find perimeter of △ABC.
The correct Answer is:15 cm
To find the perimeter of triangle ABC, which is similar to triangle DEF, we can follow these steps:
Step 1: Understand the Similarity of Triangles
Since triangle ABC is similar to triangle DEF, the ratios of the lengths of corresponding sides are equal.
Step 2: Identify the Given Values
From the problem, we have:
- DE = 3 cm
- EF = 2 cm
- DF = 2.5 cm
- BC = 4 cm
Step 3: Set Up the Ratios
Using the similarity of the triangles, we can set up the following ratios for the corresponding sides:
- AB / DE = BC / EF
- AC / DF = BC / EF
Step 4: Calculate AB
Using the ratio of sides:
ABDE=BCEF
Substituting the known values:
AB3=42
This simplifies to:
AB3=2
Now, cross-multiply to find AB:
AB=2×3=6 cm
Step 5: Calculate AC
Now, we can find AC using the ratio:
ACDF=BCEF
Substituting the known values:
AC2.5=42
This simplifies to:
AC2.5=2
Cross-multiply to find AC:
AC=2×2.5=5 cm
Step 6: Calculate the Perimeter of Triangle ABC
Now that we have all the sides of triangle ABC:
- AB = 6 cm
- BC = 4 cm
- AC = 5 cm
We can find the perimeter:
Perimeter=AB+BC+AC
Substituting the values:
Perimeter=6+4+5=15 cm
Final Answer
The perimeter of triangle ABC is 15 cm.
---
Since triangle ABC is similar to triangle DEF, the ratios of the lengths of corresponding sides are equal.
From the problem, we have:
- DE = 3 cm
- EF = 2 cm
- DF = 2.5 cm
- BC = 4 cm
Using the similarity of the triangles, we can set up the following ratios for the corresponding sides:
- AB / DE = BC / EF
- AC / DF = BC / EF
Using the ratio of sides:
ABDE=BCEF
Substituting the known values:
AB3=42
This simplifies to:
AB3=2
Now, cross-multiply to find AB:
AB=2×3=6 cm
Now, we can find AC using the ratio:
ACDF=BCEF
Substituting the known values:
AC2.5=42
This simplifies to:
AC2.5=2
Cross-multiply to find AC:
AC=2×2.5=5 cm
Now that we have all the sides of triangle ABC:
- AB = 6 cm
- BC = 4 cm
- AC = 5 cm
Perimeter=AB+BC+AC
Substituting the values:
Perimeter=6+4+5=15 cm
The perimeter of triangle ABC is 15 cm.
Topper's Solved these Questions
- TRIANGLESBOOK - EDUCART PUBLICATIONCHAPTER - TRIANGLESEXERCISE - SHORT ANSWER (SA-II) TYPE QUESTIONS
21 Videos
- TRIANGLESBOOK - EDUCART PUBLICATIONCHAPTER - TRIANGLESEXERCISE - LONG ANSWER TYPE QUESTIONS
10 Videos
- TRIANGLESBOOK - EDUCART PUBLICATIONCHAPTER - TRIANGLESEXERCISE - VERY SHORT QUESTIONS
10 Videos
- SURFACE AREAS AND VOLUMESBOOK - EDUCART PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS
30 Videos
Similar Questions
Knowledge Check
In figure ,DE||BC in triangle ABC such that BC = 8 cm , AB = 6 cm and DA = 1.5 cm .find DE.
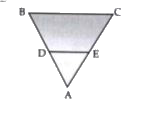 A2 cmB3 cmC4 cmD5 cm
A2 cmB3 cmC4 cmD5 cm
In the given fig. AP = 4 cm, BQ = 6 cm and AC = 9 cm. Find the semi perimeter of ΔABC.
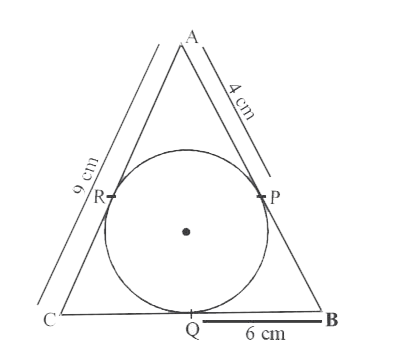
View SolutionIf ABC and DEF are similar triangles such that AB=3cm , BC=2cm CA=2.5cm and EF=4cm , write the perimeter of DEF .
View SolutionIf triangle ABC is similar to triangle DEF such that 2AB = DE and BC = 8 cm then EF is .
View SolutionP and Q are the points on the sides DE and DF of a triangle DEF such that DP = 5 cm, DE = 15 cm, DQ = 6 cm and QF = 18 cm. Is PQ||EF? Give reasons for your answer
View SolutionD and E are respectively the points on the sides AB and AC of a triangle ABC such that AE = 5 cm, AC= 7.5 cm, DE= 4.2 cm and DE||BC. Then find length of BC.
View Solution△ABC~△EDF and ar(△ABC):ar(△DEF)=4:9. If AB = 6 cm, BC = 8 cm and AC = 10 cm, then DF is equal to :
△ABC~△EDF और ar(△ABC):ar(△DEF)=4:9 है। यदि AB = 6 सेमी, BC = 8 सेमी तथा AC = 10 सेमी है, तो DF का मान क्या होगा ?
View SolutionIn a △ABC, DE is parallel to BC, AD = 3 cm, AE = 4cm and AC = 10 cm, then the value of BD in centimetres, is:
△ABC में, DE, BC & समानांतर है, AD = 3 cm, AE= 4cm और AC = 10 cm, फिर BD (सेंटीमीटर में) मान है:
View Solution
