Early crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii.
Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
If the anion is considered as the packing atom in the crystal, then the smaller catin fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbour anions then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.
Coordiantion numberGeometryρ=rcationramion2linear0−0.1553triangular0.155−0.2254tetrahedral0.225−0.4144square planar0.414−0.7326octahedral0.414−0.7328cubic0.732−1.012cuboctahedral1.0
(Source : Ionic Radii and Radius Ratios. (2021, June 8). Retrieved June 29, 2021, from https://chem.ibretexts.org/@go/page/183346)
A solid AB has square planar structure. If the radius of cation A+ is 120 pm, calculate the maximum possible value of anion B−.
240 pm
270 pm
280 pm
290 pm
The correct Answer is:D
To solve the problem, we need to determine the maximum possible value of the anion radius B− for a solid AB that has a square planar structure. The radius of the cation A+ is given as 120 pm.
1. Identify the Coordination Geometry and Radius Ratio:
- The problem states that the solid AB has a square planar structure. According to the provided table, the radius ratio ρ for square planar coordination is between 0.414 and 0.732.
2. Set Up the Equations:
- Let the radius of the anion B− be x.
- The radius ratio ρ is defined as:
ρ=rcationranion=120pmx
3. Calculate the Maximum Anion Radius Using the Lower Limit:
- Using the lower limit of the radius ratio (0.414):
0.414=120pmx
- Rearranging gives:
x=120pm0.414≈289.8pm
4. Calculate the Minimum Anion Radius Using the Upper Limit:
- Using the upper limit of the radius ratio (0.732):
0.732=120pmx
- Rearranging gives:
x=120pm0.732≈164.0pm
5. Determine the Maximum Possible Value of the Anion Radius:
- The maximum possible value of the anion radius B− corresponds to the lower limit of the radius ratio, which we calculated as approximately 289.8 pm.
6. Final Answer:
- The maximum possible value of the anion B− is approximately 290 pm.
- The problem states that the solid AB has a square planar structure. According to the provided table, the radius ratio ρ for square planar coordination is between 0.414 and 0.732.
- Let the radius of the anion B− be x.
- The radius ratio ρ is defined as:
ρ=rcationranion=120pmx
- Using the lower limit of the radius ratio (0.414):
0.414=120pmx
- Rearranging gives:
x=120pm0.414≈289.8pm
- Using the upper limit of the radius ratio (0.732):
0.732=120pmx
- Rearranging gives:
x=120pm0.732≈164.0pm
- The maximum possible value of the anion radius B− corresponds to the lower limit of the radius ratio, which we calculated as approximately 289.8 pm.
- The maximum possible value of the anion B− is approximately 290 pm.
Topper's Solved these Questions
Similar Questions
Early crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii. Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
If the anion is considered as the packing atom in the crystal, then the smaller cation fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbour anions then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.
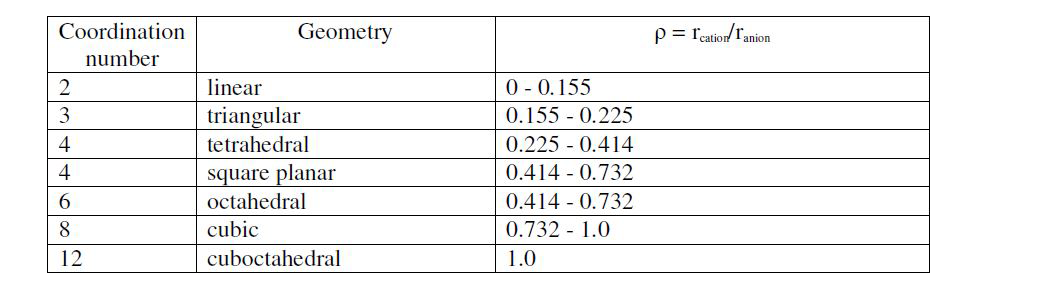
A "good fit" is considered to be one where the cation can touch:
View SolutionEarly crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii. Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
If the anion is considered as the packing atom in the crystal, then the smaller cation fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbour anions then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.

The radius of Ag+ ion is 126pm and of I− ion is 216pm. The coordination number of Ag+ ion is:
View Solution
Knowledge Check
Early crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii.
Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
If the anion is considered as the packing atom in the crystal, then the smaller catin fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbour anions then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.
Coordiantion numberGeometryρ=rcationramion2linear0−0.1553triangular0.155−0.2254tetrahedral0.225−0.4144square planar0.414−0.7326octahedral0.414−0.7328cubic0.732−1.012cuboctahedral1.0
(Source : Ionic Radii and Radius Ratios. (2021, June 8). Retrieved June 29, 2021, from https://chem.ibretexts.org/@go/page/183346)
The radius of Ag+ ion is 126 pm and of I− ion is 216 pm. The coordination number of Ag+ ion is :A2B3C6D8The central maximum in the diffraction pattern of a circular aperture is known as
Athe Abbe discBthe Airy discCthe Poisson spotDthe Rayleigh spotNeutron diffraction pattern is used to determine
ADensity of solidsBAtomic number of elementsCCrystal structure of solidDRefractive index of liquid
Early crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii. Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
If the anion is considered as the packing atom in the crystal, then the smaller cation fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbour anions then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.
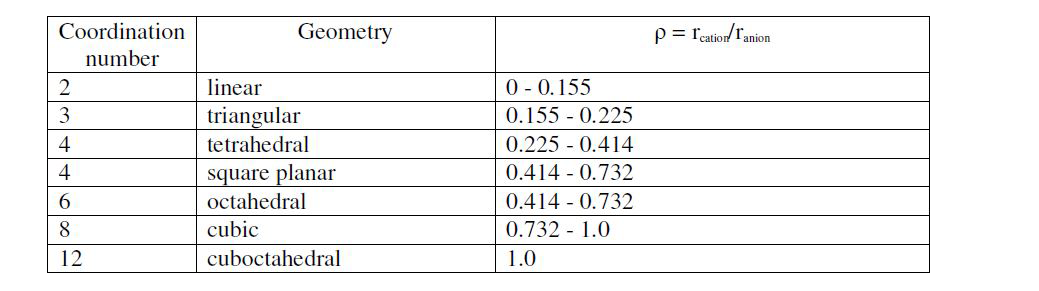
A solid AB has square planar structure. If the radius of cation A+ is 120pm,Calculate the maximum possible value of anion B−
View SolutionThe given structure was proposed with the help of X-ray diffraction data produced by:
View Solution(a) Explain how the intensity of diffraction pattern changes as the order (n) of the diffraction band varies.
(b) Two wavelengths of sodium light 590 nm and 596 nm are used in turn to study the diffraction at a single slit of size 4mm. The distance between the slit and screen is 2m. Calculate the separation between the positions of the first maximum of the diffraction pattern obtained in the two cases.
View SolutionIn a diffraction pattern the width of any fringe is
View SolutionThe centre of the diffraction pattern in Fraunhofer diffraction is always
View Solution

