Early crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii.
Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
If the anion is considered as the packing atom in the crystal, then the smaller catin fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbour anions then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.
Coordiantion numberGeometryρ=rcationramion2linear0−0.1553triangular0.155−0.2254tetrahedral0.225−0.4144square planar0.414−0.7326octahedral0.414−0.7328cubic0.732−1.012cuboctahedral1.0
(Source : Ionic Radii and Radius Ratios. (2021, June 8). Retrieved June 29, 2021, from https://chem.ibretexts.org/@go/page/183346)
The radius of Ag+ ion is 126 pm and of I− ion is 216 pm. The coordination number of Ag+ ion is :
2
3
6
8
The correct Answer is:C
To find the coordination number of the Ag⁺ ion based on the given radii of the Ag⁺ and I⁻ ions, we can follow these steps:
Step 1: Identify the radii of the ions
- The radius of the Ag⁺ ion is given as 126 pm.
- The radius of the I⁻ ion is given as 216 pm.
Step 2: Calculate the radius ratio
- The radius ratio (ρ) is calculated using the formula:
ρ=rcationranion
- Substituting the values:
ρ=126 pm216 pm≈0.5833
Step 3: Determine the coordination number based on the radius ratio
- From the table provided in the question, we can see the ranges for coordination numbers based on the radius ratio:
- 0 - 0.155: Coordination number = 2 (Linear)
- 0.155 - 0.225: Coordination number = 3 (Triangular)
- 0.225 - 0.414: Coordination number = 4 (Tetrahedral)
- 0.414 - 0.732: Coordination number = 6 (Octahedral)
- 0.732 - 1.0: Coordination number = 8 (Cubic)
- 1.0: Coordination number = 12 (Cuboctahedral)
- Our calculated radius ratio of approximately 0.5833 falls within the range of 0.414 - 0.732.
Step 4: Conclude the coordination number
- Since the radius ratio of 0.5833 corresponds to a coordination number of 6, we conclude that the coordination number of the Ag⁺ ion is 6.
Final Answer
- The coordination number of the Ag⁺ ion is 6.
---
- The radius of the Ag⁺ ion is given as 126 pm.
- The radius of the I⁻ ion is given as 216 pm.
- The radius ratio (ρ) is calculated using the formula:
ρ=rcationranion
- Substituting the values:
ρ=126 pm216 pm≈0.5833
- From the table provided in the question, we can see the ranges for coordination numbers based on the radius ratio:
- 0 - 0.155: Coordination number = 2 (Linear)
- 0.155 - 0.225: Coordination number = 3 (Triangular)
- 0.225 - 0.414: Coordination number = 4 (Tetrahedral)
- 0.414 - 0.732: Coordination number = 6 (Octahedral)
- 0.732 - 1.0: Coordination number = 8 (Cubic)
- 1.0: Coordination number = 12 (Cuboctahedral)
- Since the radius ratio of 0.5833 corresponds to a coordination number of 6, we conclude that the coordination number of the Ag⁺ ion is 6.
- The coordination number of the Ag⁺ ion is 6.
Topper's Solved these Questions
Similar Questions
Early crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii. Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
If the anion is considered as the packing atom in the crystal, then the smaller cation fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbour anions then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.
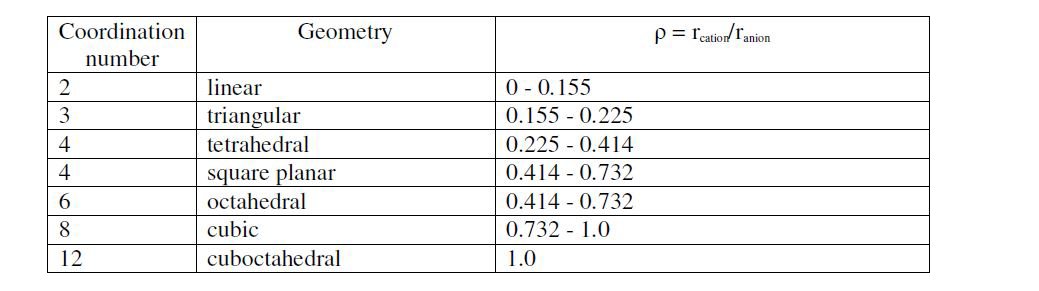
A "good fit" is considered to be one where the cation can touch:
View SolutionEarly crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii. Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
If the anion is considered as the packing atom in the crystal, then the smaller cation fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbour anions then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.
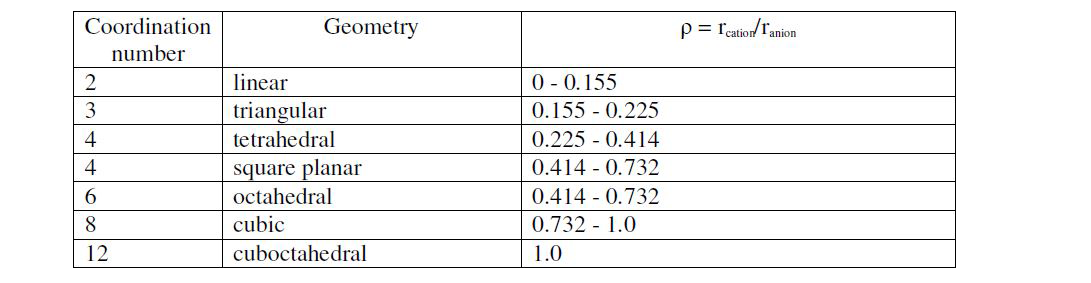
The radius of Ag+ ion is 126pm and of I− ion is 216pm. The coordination number of Ag+ ion is:
View Solution
Knowledge Check
Early crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii.
Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
If the anion is considered as the packing atom in the crystal, then the smaller catin fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbour anions then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.
Coordiantion numberGeometryρ=rcationramion2linear0−0.1553triangular0.155−0.2254tetrahedral0.225−0.4144square planar0.414−0.7326octahedral0.414−0.7328cubic0.732−1.012cuboctahedral1.0
(Source : Ionic Radii and Radius Ratios. (2021, June 8). Retrieved June 29, 2021, from https://chem.ibretexts.org/@go/page/183346)
A solid AB has square planar structure. If the radius of cation A+ is 120 pm, calculate the maximum possible value of anion B−.A240 pmB270 pmC280 pmD290 pmThe central maximum in the diffraction pattern of a circular aperture is known as
Athe Abbe discBthe Airy discCthe Poisson spotDthe Rayleigh spotNeutron diffraction pattern is used to determine
ADensity of solidsBAtomic number of elementsCCrystal structure of solidDRefractive index of liquid
Early crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii. Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
If the anion is considered as the packing atom in the crystal, then the smaller cation fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbour anions then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.
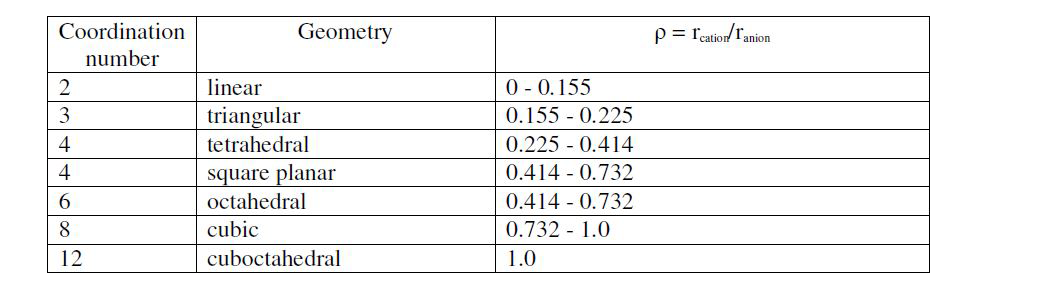
A solid AB has square planar structure. If the radius of cation A+ is 120pm,Calculate the maximum possible value of anion B−
View SolutionThe given structure was proposed with the help of X-ray diffraction data produced by:
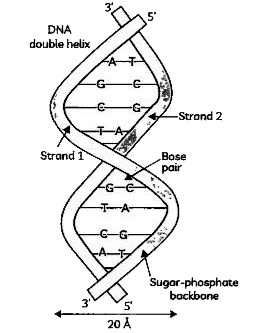
View Solution(a) Explain how the intensity of diffraction pattern changes as the order (n) of the diffraction band varies.
(b) Two wavelengths of sodium light 590 nm and 596 nm are used in turn to study the diffraction at a single slit of size 4mm. The distance between the slit and screen is 2m. Calculate the separation between the positions of the first maximum of the diffraction pattern obtained in the two cases.
View SolutionIn a diffraction pattern the width of any fringe is
View SolutionThe centre of the diffraction pattern in Fraunhofer diffraction is always
View Solution

