In figure , if AB||DC and AC, PQ intersect each other at the point O. Prove that OA.CQ=OC.AP.
The correct Answer is:OA×CQ=OC×AP
Step by step video, text & image solution for In figure , if ABabs()DC and AC, PQ intersect each other at the point O. Prove that OA.CQ=OC.AP. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER -6 EXERCISE - Part - B (Section - V)6videos
SAMPLE PAPER -6
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER -6 EXERCISE - Part - B (Section - III)9videos
SAMPLE PAPER -6
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER -5EXERCISE - SECTION-C11videos
SAMPLE PAPER -5
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 01EXERCISE - PART-B (SECTION-V)4videos
SAMPLE PAPER 01
Similar Questions
In the figure, two chords AB and CD intersect each other at the point P.
Prove that : AP. PB = CP. DP
View SolutionIn the figure, two chords AB and CD intersect each other at the point P.
Prove that : ΔAPC~ΔDPB
View SolutionIn the figure the bisectors of ∠P and ∠Q intersect to each other at a point R. Prove that ∠PRQ=90∘.
View SolutionABCD is a trapezium in which AB||DC and its diagonals intersect each other as the point O. Show that AOBO=CODO.
View SolutionPQandRS are two parallel chords of a circle and lines RPandSQ intersect each other at O as shown in Figure. Prove that OP=OQ.
View SolutionPQ and RS are two parallel chords of a circle and lines RP and SQ intersect each other at O as shown in Figure. Prove that OP=OQ
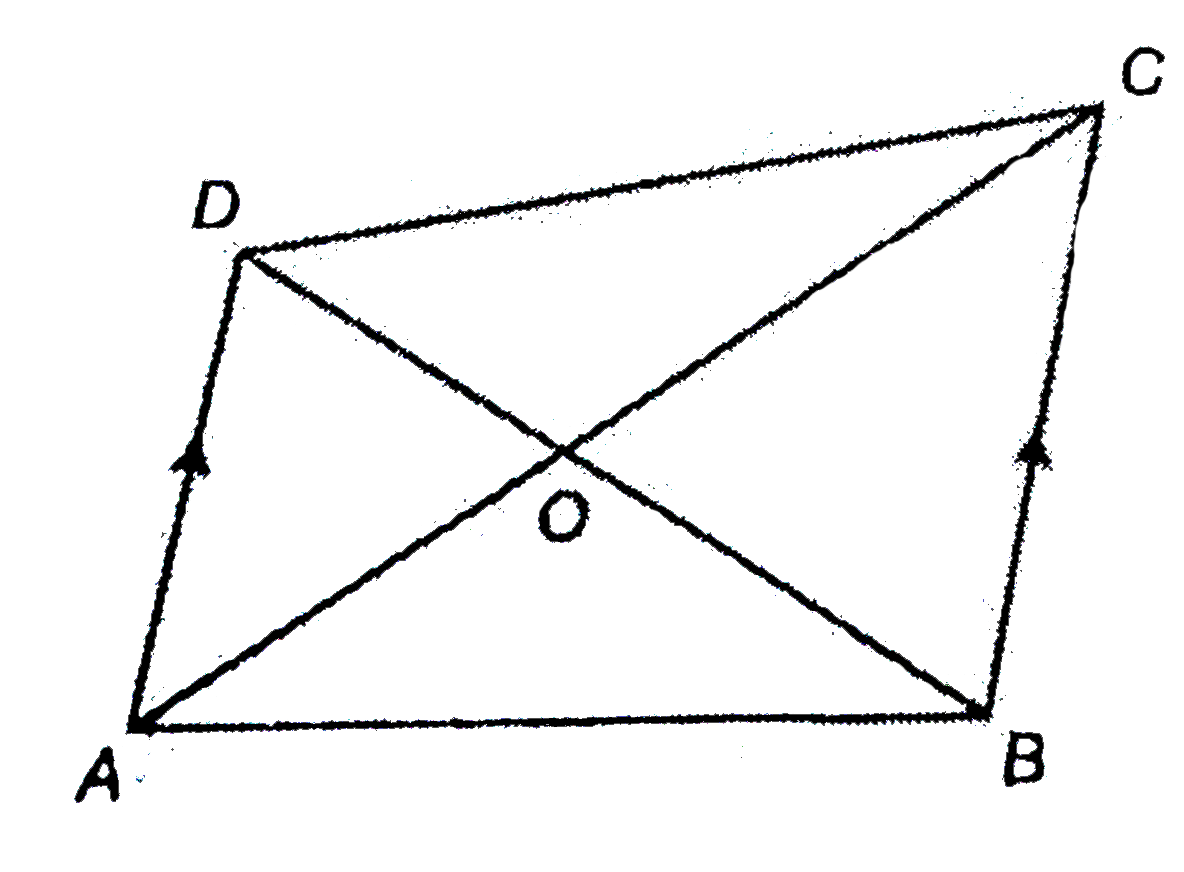
View SolutionIn the adjoining figure, ABCD is a quadrilateral in which AD∣∣BC. AC and BD intersect each other at point 'O'. Prove that:
area of ΔCOD= area of ΔABO
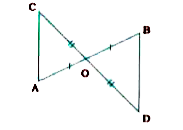
View SolutionIn the given figure AB and CD bisect each other at O. Prove that AC = BD.
View SolutionTriangle ABC is an isosceles triangle with AB=AC. Bisectors of ∠Band∠C intersect each other at O. join A−O and prove that
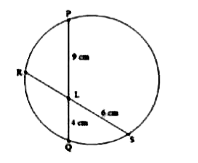
OB=OCView SolutionIn the given figure, chords PQ and RS intersect each other at point L. Find the lenth of RL.
View Solution