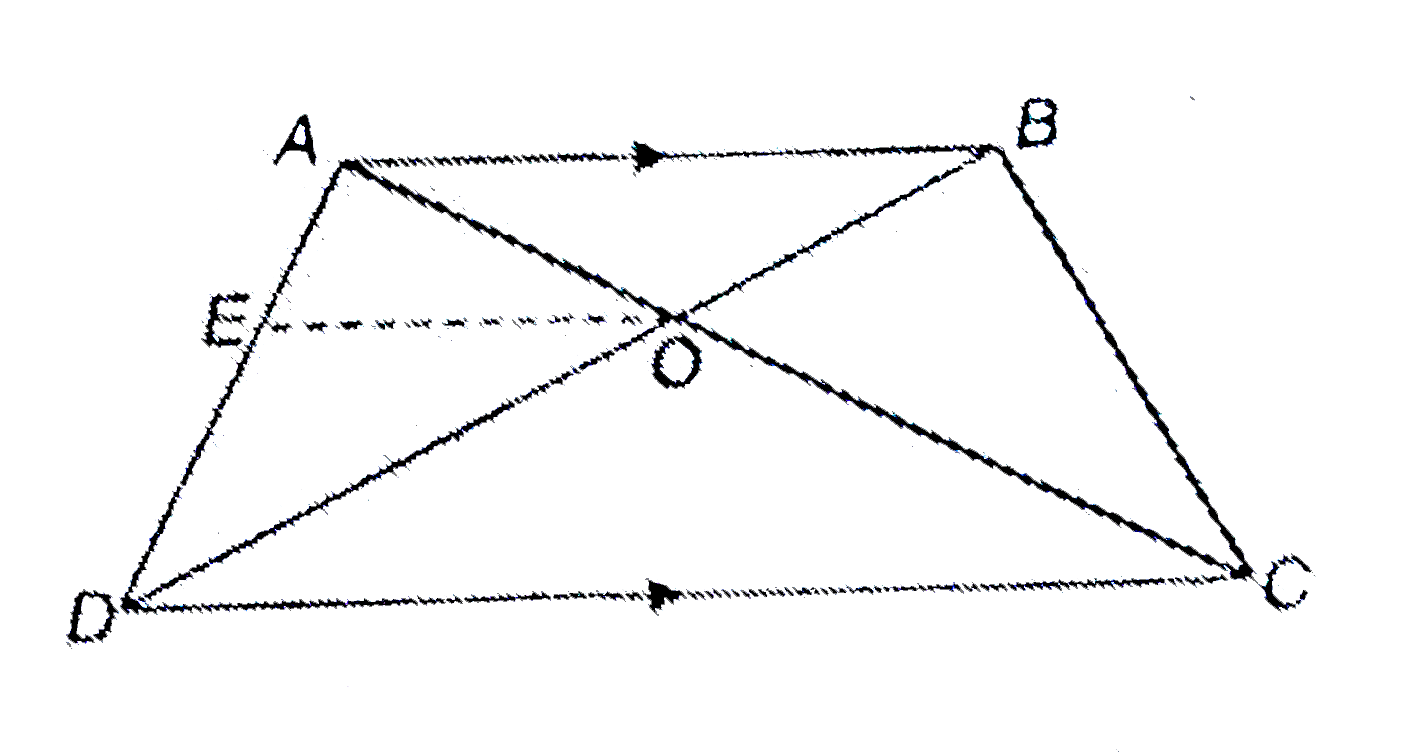
ABCD is a trapezium in which AB||DC and its diagonals intersect each other as the point O. Show that $\frac{A O}{B O} = \frac{C O}{D O}$ .

Text Solution

Verified by Experts

The correct Answer is:13 m

|

Updated on:21/07/2023

Class 10 MATHS QUESTION BANK

Topper's Solved these Questions

BOOK - MBD -HARYANA BOARDCHAPTER - MBD NEW STYPE MODEL TEST PAPER - 2EXERCISE - SET - A (SECTION -C)
5videos
MBD NEW STYPE MODEL TEST PAPER - 2
BOOK - MBD -HARYANA BOARDCHAPTER - MBD NEW STYPE MODEL TEST PAPER - 2EXERCISE - SET - A (SECTION -D)
5videos
MBD NEW STYPE MODEL TEST PAPER - 2
BOOK - MBD -HARYANA BOARDCHAPTER - MBD NEW STYPE MODEL TEST PAPER - 2EXERCISE - SET - D (SECTION - D)
6videos
MBD NEW STYPE MODEL TEST PAPER - 2
BOOK - MBD -HARYANA BOARDCHAPTER - MBD NEW STYLE MODEL TEST PAPER -1 EXERCISE - SET - D (SECTION - D)
4videos
MBD NEW STYLE MODEL TEST PAPER -1
BOOK - MBD -HARYANA BOARDCHAPTER - PAIR OF LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - SHORT ANSWER TYPE QUESTIONS
20videos
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES

Similar Questions

Knowledge Check

Question 1 - Select One
ABCD is a trapezium in which $A B ∣ ∣ C D$ and $A B = 2 C D$ . It its diagonals intersect each other at O then ratio of the area of triangle AOB and COD is
A $1 : 2$
B $2 : 1$
C $1 : 4$
D $4 : 1$
Question 2 - Select One
ABCD is a trapezium in which AB||CD and AB=2CD. If its diagonals intersect each other at O, then ratio of areas of trianlges AOB and COD is :
A $1 : 4$
B $1 : 2$
C $4 : 1$
D $2 : 1$
Question 3 - Select One
ABCD is a trapezium in which AB||CD and AB=2CD. If its diagonals intersect each other at O, then ratio of areas of trianlges AOB and COD is :
A1:4
B1:2
C4:1
D2:1

MBD -HARYANA BOARD-MBD NEW STYPE MODEL TEST PAPER - 2-SET - A (SECTION -B)

Home
Ask Doubt
Profile