O is the centre of the circle of radius 6 cm and P is the mid -point of a chord AB .The length OP is 3 cm. The area (in sq cm ) of △AOB is :
26π
24π
20π
18π
The correct Answer is:B
To find the area of triangle AOB, we can follow these steps:
Step 1: Understand the given information
- O is the center of the circle with a radius of 6 cm.
- P is the midpoint of the chord AB.
- The length OP is 3 cm.
Step 2: Visualize the triangle
Draw a circle with center O. Mark the radius OA = OB = 6 cm. Draw the chord AB and mark its midpoint P. Connect OP, which is perpendicular to AB.
Step 3: Use the properties of triangles
Since OP is perpendicular to AB, triangle AOB is divided into two right triangles, AOP and BOP. The height from O to the chord AB is OP = 3 cm.
Step 4: Apply the Pythagorean theorem
In triangle AOP:
- OA (hypotenuse) = 6 cm (radius)
- OP (one side) = 3 cm (height)
- AP (the other side) = x (unknown)
Using the Pythagorean theorem:
OA2=OP2+AP2
62=32+x2
36=9+x2
x2=36−9
x2=27
x=√27=3√3 cm
Step 5: Calculate the area of triangle AOB
The area of triangle AOB can be calculated using the formula:
Area=12×base×height
Here, the base AB = 2 * AP = 2x = 2(3\sqrt{3}) = 6\sqrt{3} cm, and the height OP = 3 cm.
Thus, the area of triangle AOB is:
Area=12×(6√3)×3
Area=12×18√3
Area=9√3 cm2
Final Answer
The area of triangle AOB is 9√3 cm2.
---
- O is the center of the circle with a radius of 6 cm.
- P is the midpoint of the chord AB.
- The length OP is 3 cm.
Draw a circle with center O. Mark the radius OA = OB = 6 cm. Draw the chord AB and mark its midpoint P. Connect OP, which is perpendicular to AB.
Since OP is perpendicular to AB, triangle AOB is divided into two right triangles, AOP and BOP. The height from O to the chord AB is OP = 3 cm.
In triangle AOP:
- OA (hypotenuse) = 6 cm (radius)
- OP (one side) = 3 cm (height)
- AP (the other side) = x (unknown)
OA2=OP2+AP2
62=32+x2
36=9+x2
x2=36−9
x2=27
x=√27=3√3 cm
The area of triangle AOB can be calculated using the formula:
Area=12×base×height
Area=12×(6√3)×3
Area=12×18√3
Area=9√3 cm2
The area of triangle AOB is 9√3 cm2.
Topper's Solved these Questions
- SAMPLE PAPER SOLVED 9 Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER SOLVED 9 Exercise:Part - B (Section -III)
Explore 8 Videos
- SAMPLE PAPER SOLVED 9 Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER SOLVED 9 Exercise:Part - B (Section -IV)
Explore 11 Videos
- SAMPLE PAPER SOLVED 9 Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER SOLVED 9 Exercise:Part - B (Section -V)
Explore 4 Videos
- SAMPLE PAPER SOLVED 10Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER SOLVED 10Exercise:PART - B ( SECTION - V )
Explore 5 Videos
- SAMPLE PAPER SOLVED 4 Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER SOLVED 4 Exercise:SECTION - C
Explore 10 Videos
Similar Questions
In CERN , some work is carried out for developing an accurate and fast numerical method that can calculate natural gas flow in a pipeline under non isothermal steady -state conditions .
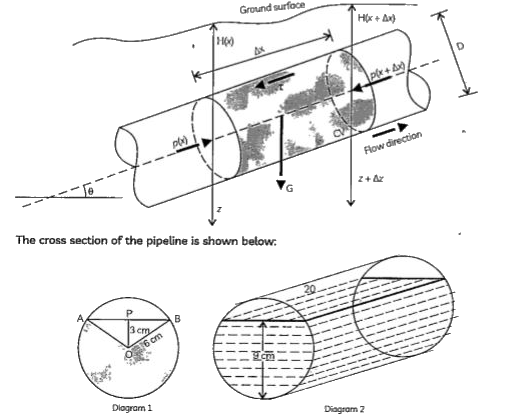
In Diagram 1, O is the centre of the circle of radius 6 cm and P is the mid -point of the chord AB .The length OP is 3 cm.
The area (in sq cm ) of ΔAOB is :
View SolutionIn the given figure, O is the centre of a circle of radius 13 cm and AB is a chord perpendicular to OD. If CD = 8 cm, then what is the length (in cm) of AB?
View SolutionThe radius of a circle is 5 cm and the distance of a chord from the centre is 3 cm . Find the length of the chord.
View SolutionIn a circle of radius 10 cm, a chord is at a distance of 6 cm from the centre. The length of chord is
View SolutionThe given figure shows a circle with centre O. P is mid-point of chord AB. Show that OP is perpendicular to AB.

View SolutionO is the centre of the circle ABC, radius 5 cm, AB = 8 cm, AC = 6 cm. Calculate the lengths of the perpendiculars OP, OQ from O to AB, AC.
View SolutionThere is a circle of radius 5 cm. There are two chords AB and AC OF equal length = 6 cm . Find the length of chord BC .
View SolutionIn a circle of radius 5 cm, AB and Ac are two chords of 6cm each. Find the length of the chord BC.
View SolutionThere is a circle of radius 5 cm. There are two chords AB and AC OF equal length = 6 cm . Find the length of chord BC .
View SolutionPT is a tangent to a circle with centre O and radius 6cm. If PT is 8cm then length of OP is:
View Solution

