O is the centre of the circle ABC, radius 5 cm, AB = 8 cm, AC = 6 cm. Calculate the lengths of the perpendiculars OP, OQ from O to AB, AC.
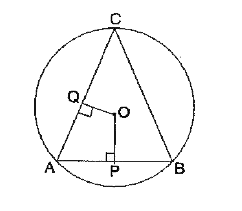
3 cm, 4 cm
4 cm, 3 cm
2 cm, 3 cm
3.5 cm, 2.5 cm
The correct Answer is:A
Step by step video, text & image solution for O is the centre of the circle ABC, radius 5 cm, AB = 8 cm, AC = 6 cm. Calculate the lengths of the perpendiculars OP, OQ from O to AB, AC. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLES Book:S CHAND IIT JEE FOUNDATIONChapter:CIRCLES Exercise:UNIT TEST
Explore 20 Videos
- CIRCLES Book:S CHAND IIT JEE FOUNDATIONChapter:CIRCLES Exercise:QUESTION BANK
Explore 25 Videos
- AVERAGE Book:S CHAND IIT JEE FOUNDATIONChapter:AVERAGE Exercise:UNIT TEST -3
Explore 20 Videos
- CIRCUMFERENCE AND AREA OF A CIRCLE Book:S CHAND IIT JEE FOUNDATIONChapter:CIRCUMFERENCE AND AREA OF A CIRCLE Exercise:SELF ASSESSMENT SHEET - 22
Explore 10 Videos
Similar Questions
Knowledge Check
In △ABC,AB=6cm,AC=8cm,andBC=9cm. The length of median AD is :
A√3172cmB√1192cmC√1152cmD√3132cmO is the centre of the circle of radius 6 cm and P is the mid -point of a chord AB .The length OP is 3 cm. The area (in sq cm ) of △AOB is :
A26πB24πC20πD18πO is the circumcentre of the isosceles ΔABC. Given that AB = AC = 17 cm and BC = 6 cm. The radius of the circle is
A3.015 cm.B3.205 cm.C3.025 cm.D3.125 cm.
In a circle of radius 5 cm, AB and Ac are two chords of 6cm each. Find the length of the chord BC.
View SolutionO is the circumcentre of the isosceles ΔABC. Given that AB = AC = 17 cm and BC = 6 cm. The radius of the circle is
View SolutionIn a circle of radius 5 cm, AB and AC are two chords such that AB=AC=6cm. Find the length of the chord BC
View SolutionIn the given figure, O is the centre of the circle. Radius of the circle is 17 cm. lf OC=8cm, then the length of the chord AB is :
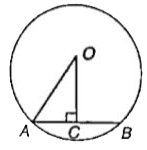
View SolutionIn a triangle ABC, BC = 5 cm, AC = 12 cm and AB = 13 cm. The length of the altitude drawn from B on AC is -----
View Solution
