Theorem 6.1 : If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Both A and R are true R is the correct explanation for A.
Both A and R are true nad R is not correct explanation for A.
A is true but R is false.
A is false but R is true.
The correct Answer is:A
Step by step video, text & image solution for Theorem 6.1 : If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - CASE - BASED MCQs
15 Videos
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - EXAMPLE
2 Videos
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - Self Assessment
4 Videos
- SURFACE AREAS AND VOLUMES BOOK - OSWAL PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - BOARD CORNER (LONG ANSWER TYPE QUESTIONS)
9 Videos
Similar Questions
Prove that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
View SolutionProve that, if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Using the above result, do the following:
In Fig. 7 .45 DE||BC and BD = CE. Prove that ΔABC is an isosceles triangle.
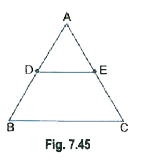
View Solution
Knowledge Check
Thales theorem is given by a greek mathematician. According to this theorem, if a line is drawn parallel to one side of a triangle then it divides the other two sides in the same ratio. This theorem is also known as Basic Proportionality Theorem.
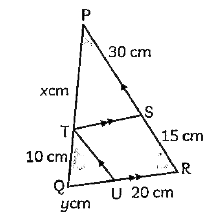
Here, the value of x is :A20 cmB15 cmC5 cmD10 cm
If a line is drawn to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
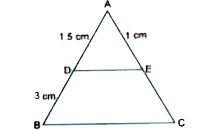
View SolutionIf a line is drawn parallel to one side of a triangle to intersect the other two sides in disinct points, the other two sides are divided in the same ratio. Using this theoure. Find EC in if DE∣∣BC.
View SolutionBasic proportionality Theorem or Thales Theorem - If a line is drawn parallel to one side of a triangle intersecting the other two sides; then it divides the two sides in the same ratio.
View SolutionProve that , "If a line parallel to a side of a triangle intersects the remaining sides in two distinct points then the line divides the sides in the same proportion".
View Solution(B) Solve any two of the following subquestions :
Prove that following statement, " If a line parallel to a side of a Delta intersects the remaining sides in two distinct points , then the line divides the sides in the same proportion . "
View SolutionTheorem 6.2 : If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
View SolutionTheorem 8.10 : The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.
View Solution
