If a line is drawn parallel to one side of a triangle to intersect the other two sides in disinct points, the other two sides are divided in the same ratio. Using this theoure. Find EC in if DE∣∣BC.
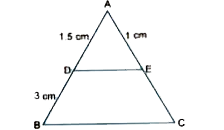
The correct Answer is:2 cm
Step by step video, text & image solution for If a line is drawn parallel to one side of a triangle to intersect the other two sides in disinct points, the other two sides are divided in the same ratio. Using this theoure. Find EC in if DE||BC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- POST-MID TEAM TEST PAPERBOOK - VK GLOBAL PUBLICATIONCHAPTER - POST-MID TEAM TEST PAPEREXERCISE - SECTION-C
10 Videos
- POLYNOMIALS BOOK - VK GLOBAL PUBLICATIONCHAPTER - POLYNOMIALS EXERCISE - SELF-ASSESSMENT TEST
11 Videos
- PRE-MID TERM TEST PAPERBOOK - VK GLOBAL PUBLICATIONCHAPTER - PRE-MID TERM TEST PAPEREXERCISE - SECTION-D
3 Videos
Similar Questions
If a line is drawn to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
View SolutionTheorem 6.1 : If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
View Solution
Knowledge Check
If the line DE is drawn parallel | to the base BC of a triangle ABC by Intersecting the other two sides, then which of the following is the CORRECT equation for this case.
AABDB=ACECBADAB=DBECCADDB=ECAEDADDB=AEECThales theorem is given by a greek mathematician. According to this theorem, if a line is drawn parallel to one side of a triangle then it divides the other two sides in the same ratio. This theorem is also known as Basic Proportionality Theorem.
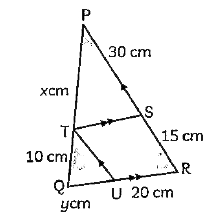
Here, the value of x is :A20 cmB15 cmC5 cmD10 cm
Prove that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
View SolutionProve that, if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Using the above result, do the following:
In Fig. 7 .45 DE||BC and BD = CE. Prove that ΔABC is an isosceles triangle.
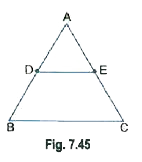
View SolutionProve that , "If a line parallel to a side of a triangle intersects the remaining sides in two distinct points then the line divides the sides in the same proportion".
View SolutionBasic proportionality Theorem or Thales Theorem - If a line is drawn parallel to one side of a triangle intersecting the other two sides; then it divides the two sides in the same ratio.
View SolutionThe line drawn from the midpoint of one side of a triangle parallel to another side bisects the third side.
View SolutionThe line drawn through the mid-point of one side of a triangle, parallel to another side, intersects the third side at its mid-point.
View Solution
