In ΔDEFandΔPQR, if PQ =DE, EF=PR and FD =QR, then
ΔDEF≅ΔRPQ
ΔDEF≅ΔQPR
ΔDEF≅ΔQRP
ΔDEF≅ΔPQR
The correct Answer is:B
To determine the congruence of triangles DEF and PQR given the conditions PQ = DE, EF = PR, and FD = QR, we can follow these steps:
1. Identify the triangles: We have two triangles, triangle DEF and triangle PQR.
2. List the given equalities:
- PQ = DE
- EF = PR
- FD = QR
3. Understand the congruence criterion: The criterion we will use is the Side-Side-Side (SSS) congruence theorem. This theorem states that if three sides of one triangle are equal to three sides of another triangle, then the two triangles are congruent.
4. Apply the SSS criterion:
- From the given information:
- Side PQ corresponds to side DE.
- Side EF corresponds to side PR.
- Side FD corresponds to side QR.
- Since all three pairs of corresponding sides are equal, we can conclude that triangle DEF is congruent to triangle PQR.
5. Conclusion: Therefore, we can write:
△DEF≅△PQR(by SSS congruence)
- PQ = DE
- EF = PR
- FD = QR
- From the given information:
- Side PQ corresponds to side DE.
- Side EF corresponds to side PR.
- Side FD corresponds to side QR.
- Since all three pairs of corresponding sides are equal, we can conclude that triangle DEF is congruent to triangle PQR.
△DEF≅△PQR(by SSS congruence)
Topper's Solved these Questions
- GEOMETRYBook:ARIHANT PUBLICATION PUNJABChapter:GEOMETRYExercise:CHAPTER EXERCISE
Explore 70 Videos
- EVALUTIONBook:ARIHANT PUBLICATION PUNJABChapter:EVALUTIONExercise:Chapter Exercise
Explore 45 Videos
- GEOMETRY AND SHAPES Book:ARIHANT PUBLICATION PUNJABChapter:GEOMETRY AND SHAPES Exercise:CHAPTER EXERCISE
Explore 43 Videos
Similar Questions
Knowledge Check
In the figure, in ΔPQRandΔTQR,PQ=TRandPR=TQ. Which of the following statements is true?
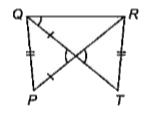 AΔPQR≅ΔRQTBΔPQR≅ΔQTRCΔPQR≅ΔTRQDΔPQR≅ΔTQR
AΔPQR≅ΔRQTBΔPQR≅ΔQTRCΔPQR≅ΔTRQDΔPQR≅ΔTQRIn ΔPQR,PQ=3 and QR=7 Then ……….holds good.
APR=4BPR=10C10>PR>4D7>PR>3In Δ PQR, PQ = 4 cm, QR = 3 cm, and RP = 3.5 cm. Δ DEF is similar to Δ PQR. If EF = 9 cm, then what is the perimeter of Δ DEF ?
A10.5 cmB21 cmC31.5 cmDCannot be determined as data is insufficient
In ΔABCand ΔDEF,AB=DEandBC=EF. Then one can infer that
ΔABC=ΔDEF, when
View SolutionΔPQRandΔTQR are on the same base QR and on the same side of QR . If PQ = TR and PR = TQ, then which of the following is correct ?
View SolutionGiven two triangles ABC and DEF. If ΔABC~ΔDEF,2AB=DE and BC = 8 cm, then find the length of EF.
View SolutionIn ΔPQR,PQ=4cm,PR=6cmandQR=3cm. Which of the following is correct?
View SolutionIn ΔPQR,PQ=4cm,PR=6cmandQR=3cm. Which of the following is correct?
View Solution