In ΔPQT,PQ=PT. The points R and S are on QT such that PR = PS. If ∠PTS=62∘and∠RPS=34∘, then measure of ∠QPR is
11∘
13∘
15∘
17∘
The correct Answer is:A
To solve the problem step by step, we will follow the reasoning provided in the video transcript.
1. Identify the Given Information:
- In triangle ΔPQT, we have PQ=PT.
- Points R and S are on line QT such that PR=PS.
- ∠PTS=62∘
- ∠RPS=34∘
2. Use the Isosceles Triangle Property:
- Since PQ=PT, triangle PQT is isosceles. Therefore, the angles opposite the equal sides are equal:
∠PQT=∠PTQ
- Let ∠PQT=∠PTQ=x.
3. Calculate ∠PQT:
- The sum of angles in triangle PQT is 180∘:
∠PQT+∠PTQ+∠PTS=180∘
x+x+62∘=180∘
2x+62∘=180∘
2x=180∘−62∘
2x=118∘
x=59∘
- Thus, ∠PQT=∠PTQ=59∘.
4. Consider Triangle PRS:
- Since PR=PS, triangle PRS is also isosceles. Therefore:
∠PRS=∠PSR
- Let ∠PRS=∠PSR=y.
5. Calculate ∠PRS:
- The sum of angles in triangle PRS is 180∘:
∠PRS+∠PSR+∠RPS=180∘
y+y+34∘=180∘
2y+34∘=180∘
2y=180∘−34∘
2y=146∘
y=73∘
- Thus, ∠PRS=∠PSR=73∘.
6. Calculate ∠QPR:
- Now, we can find ∠QPR:
∠QPR=∠PRS−∠PQT
∠QPR=73∘−59∘
∠QPR=14∘
Final Answer:
The measure of ∠QPR is 14∘.
- In triangle ΔPQT, we have PQ=PT.
- Points R and S are on line QT such that PR=PS.
- ∠PTS=62∘
- ∠RPS=34∘
- Since PQ=PT, triangle PQT is isosceles. Therefore, the angles opposite the equal sides are equal:
∠PQT=∠PTQ
- Let ∠PQT=∠PTQ=x.
- The sum of angles in triangle PQT is 180∘:
∠PQT+∠PTQ+∠PTS=180∘
x+x+62∘=180∘
2x+62∘=180∘
2x=180∘−62∘
2x=118∘
x=59∘
- Thus, ∠PQT=∠PTQ=59∘.
- Since PR=PS, triangle PRS is also isosceles. Therefore:
∠PRS=∠PSR
- Let ∠PRS=∠PSR=y.
- The sum of angles in triangle PRS is 180∘:
∠PRS+∠PSR+∠RPS=180∘
y+y+34∘=180∘
2y+34∘=180∘
2y=180∘−34∘
2y=146∘
y=73∘
- Thus, ∠PRS=∠PSR=73∘.
- Now, we can find ∠QPR:
∠QPR=∠PRS−∠PQT
∠QPR=73∘−59∘
∠QPR=14∘
The measure of ∠QPR is 14∘.
Topper's Solved these Questions
- GEOMETRYBOOK - ARIHANT PUBLICATION PUNJABCHAPTER - GEOMETRYEXERCISE - CHAPTER EXERCISE
70 Videos
- EVALUTIONBOOK - ARIHANT PUBLICATION PUNJABCHAPTER - EVALUTIONEXERCISE - Chapter Exercise
45 Videos
- GEOMETRY AND SHAPES BOOK - ARIHANT PUBLICATION PUNJABCHAPTER - GEOMETRY AND SHAPES EXERCISE - CHAPTER EXERCISE
43 Videos
Similar Questions
In △PQR,∠Q≻∠R, PS is the bisector of ∠P and PT⊥QR. If ∠SPT=28∘ and ∠R=23∘ , then the measure of ∠Q is:
त्रिभुज PQR में, ∠Q≻∠R, है तथा PS कोण P का समद्विभाजक है और PT⊥QR है । यदि ∠SPT=28∘ और ∠R=23∘ है, तो कोण Q का मान क्या है?
View SolutionIn ΔPQR it is given that = PQPR=QSSR. If ∠Q=70∘and∠R=50∘ then ∠QPS = ?
View Solution
Knowledge Check
In ΔPQT,PQ=PT. The points R and S are on QT such that PR = PS. If ∠PTS=62∘and∠RPS=34∘, then measure of ∠QPR is
A11∘B13∘C15∘D17∘In figure, if QT⊥PR,∠TQR=40∘and∠SPR=30∘, find value of y-x
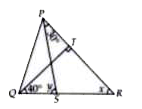 A80∘B50∘C30∘D130∘
A80∘B50∘C30∘D130∘In ΔPQR,SandT are the mid points of sides PQ and PR respectively. If ∠QPR=45∘and∠PRQ=55∘, then what is the value (in degrees) of ∠QST ?
A80B85C90D100
In △PQR, QT is perpendicular to PR and s is a point on QR such that, ∠PSQ=p∘. If ∠TQR=46∘ and ∠SPR=32∘, then the value of p is :
त्रिभुज PQR में, QT, PR पर लंब है और QR पर बिंदु s इस प्रकार पर है कि ∠PSQ=p∘ है| यदि ∠TQR=46∘ और ∠SPR=32∘ है, तो p का मान ज्ञात करें|
View Solution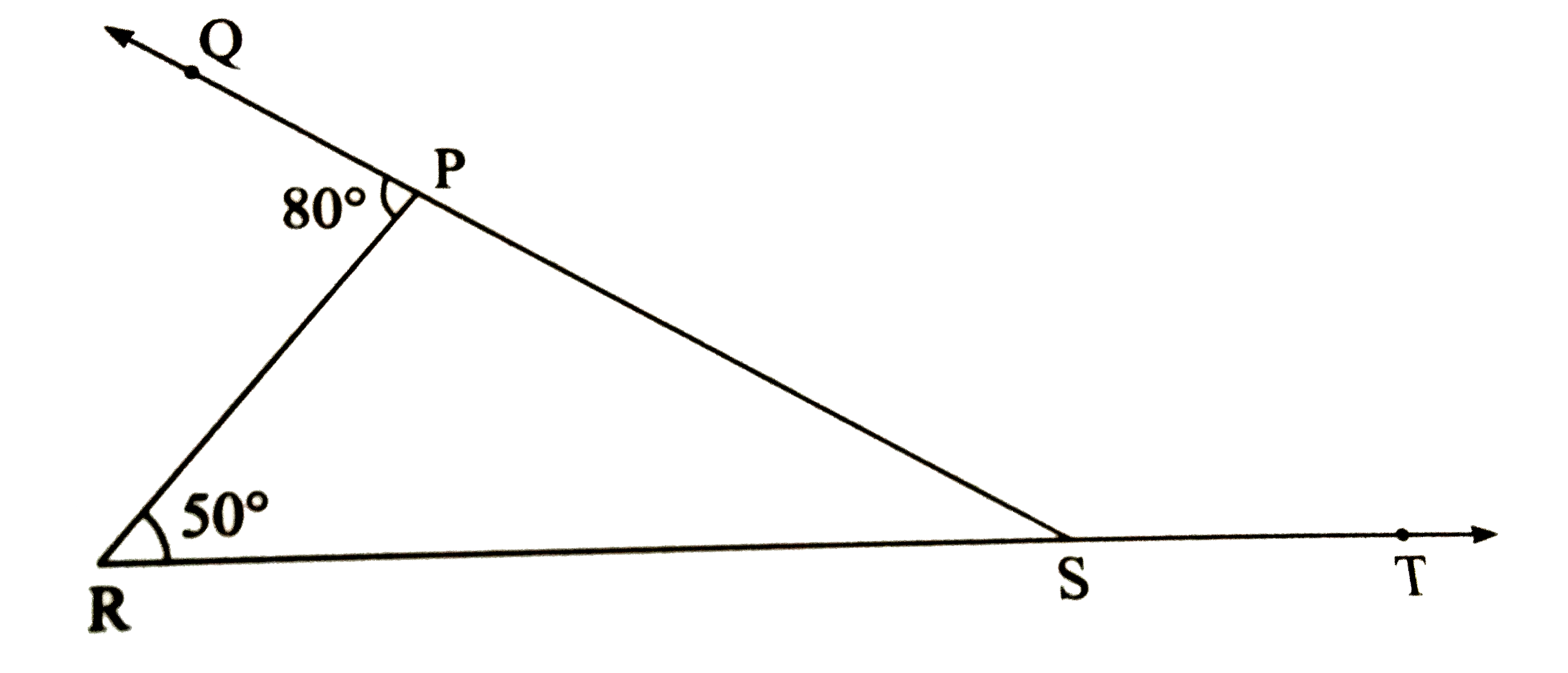
In the figure , ∠ QPR and ∠ PST are exterior angles of △ PRS . If ∠PRS=50∘ and ∠QPR=80∘ , then find measure of ∠ PST.
View SolutionIn △PQR, S and T are mid-points of PQ and PR, respectively. If ∠QPR=75∘ and ∠PQR=40∘, then ∠TSQ is:
△PQR में, S और T क्रमशः PQ और PR के मध्य-बिंदु हैं, यदि ∠QPR=75∘ और ∠PQR=40∘ तो ∠TSQ है :
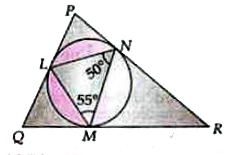
View SolutionIn the given figure PQ,QRandRP touches a given circle respectively at point I,MandN. If ∠LMN=55∘and∠MNL=50∘, then find ∠P,∠Qand∠R
View SolutionIn the figure , PQ and PR are tangent to the circle with centre O. Also, S is a point on the circle such that ∠SQC=50∘and∠SRM=60∘, then ∠QSR=
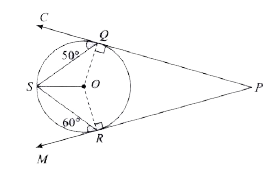
View Solution
