A radius of circle is 2.5cm AB and CD two parallel chords are at distance of 2.7cm. It AB=4.8cm, then value of CD is
4.8cm
2.4cm
3cm
4cm
The correct Answer is:C
To solve the problem, we need to find the length of the chord CD in a circle with a radius of 2.5 cm, where the distance between two parallel chords AB and CD is 2.7 cm, and the length of chord AB is 4.8 cm.
1. Draw the Circle and Chords:
- Draw a circle with a radius of 2.5 cm.
- Mark two parallel chords AB and CD such that the distance between them is 2.7 cm.
2. Identify the Midpoints:
- Let M be the midpoint of chord AB and N be the midpoint of chord CD.
- Since AB = 4.8 cm, the length of AM (or MB) will be half of AB:
AM=MB=4.82=2.4 cm
3. Use the Radius and Distance:
- The distance from the center O of the circle to chord AB is denoted as OM, and the distance from O to chord CD is ON.
- Given that the distance between the two chords is 2.7 cm, we can express this as:
ON=OM+2.7
4. Apply the Pythagorean Theorem:
- For triangle OMB (where OB is the radius):
OB2=OM2+MB2
- Substituting the known values:
(2.5)2=OM2+(2.4)2
- This simplifies to:
6.25=OM2+5.76
5. Solve for OM:
- Rearranging gives:
OM2=6.25−5.76=0.49
- Taking the square root:
OM=√0.49=0.7 cm
6. Find ON:
- Using the distance relationship:
ON=OM+2.7=0.7+2.7=3.4 cm
7. Apply Pythagorean Theorem for CD:
- For triangle OND (where OD is the radius):
OD2=ON2+ND2
- Substituting the known values:
(2.5)2=(3.4)2+ND2
- This simplifies to:
6.25=11.56+ND2
8. Solve for ND:
- Rearranging gives:
ND2=6.25−11.56=−5.31
- Since this is not possible, we need to correct our earlier calculations.
9. Recalculate:
- The correct distance from the center to chord CD should be:
ON=2.5−0.7=1.8 cm
- Now apply the Pythagorean theorem again:
OD2=ON2+ND2
- Substituting the known values:
(2.5)2=(1.8)2+ND2
- This simplifies to:
6.25=3.24+ND2
- Rearranging gives:
ND2=6.25−3.24=3.01
- Taking the square root:
ND=√3.01≈1.73 cm
10. Find Length of CD:
- Since N is the midpoint of CD:
CD=2×ND=2×1.73≈3.46 cm
Final Answer:
The length of chord CD is approximately 3.46 cm.
- Draw a circle with a radius of 2.5 cm.
- Mark two parallel chords AB and CD such that the distance between them is 2.7 cm.
- Let M be the midpoint of chord AB and N be the midpoint of chord CD.
- Since AB = 4.8 cm, the length of AM (or MB) will be half of AB:
AM=MB=4.82=2.4 cm
- The distance from the center O of the circle to chord AB is denoted as OM, and the distance from O to chord CD is ON.
- Given that the distance between the two chords is 2.7 cm, we can express this as:
ON=OM+2.7
- For triangle OMB (where OB is the radius):
OB2=OM2+MB2
- Substituting the known values:
(2.5)2=OM2+(2.4)2
- This simplifies to:
6.25=OM2+5.76
- Rearranging gives:
OM2=6.25−5.76=0.49
- Taking the square root:
OM=√0.49=0.7 cm
- Using the distance relationship:
ON=OM+2.7=0.7+2.7=3.4 cm
- For triangle OND (where OD is the radius):
OD2=ON2+ND2
- Substituting the known values:
(2.5)2=(3.4)2+ND2
- This simplifies to:
6.25=11.56+ND2
- Rearranging gives:
ND2=6.25−11.56=−5.31
- Since this is not possible, we need to correct our earlier calculations.
- The correct distance from the center to chord CD should be:
ON=2.5−0.7=1.8 cm
- Now apply the Pythagorean theorem again:
OD2=ON2+ND2
- Substituting the known values:
(2.5)2=(1.8)2+ND2
- This simplifies to:
6.25=3.24+ND2
- Rearranging gives:
ND2=6.25−3.24=3.01
- Taking the square root:
ND=√3.01≈1.73 cm
- Since N is the midpoint of CD:
CD=2×ND=2×1.73≈3.46 cm
The length of chord CD is approximately 3.46 cm.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A radius of circle is 2.5cm AB and CD two parallel chords are at distance of 2.7cm. It AB=4.8cm, then value of CD is
A4.8cmB2.4cmC3cmD4cmTwo chords AB and CD of a circle are each at distances 4 cm from the centre. Then,
AAB=CD.BAB is not equal to CD.CAB there is no relation between CD.DAB is greater than CD.In the given figureAB and CD are two parallel chords of a circle with centre O and radius 5 cm. Also, AB = 8 cm andCD = 6cm. If OP perpendicular to AB andOQ perpendicular to CD,then determine the length of PQ
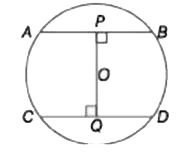 A7 cmB10 cmC8 cmDNone of these
A7 cmB10 cmC8 cmDNone of these
In a circle of radius 5 cm, AB and CD are two parallel chords of lengths 8 cm and 6 cm respectively. Calculate the distance between the chords if they are
(i) on the same side of the centre.
(ii) on the opposite sides of the centre.
View SolutionAt one end A of a diameter AB of a circle of radius 13 cm , tangent ,XAY is drawn to the circle . A chord CD is parallel to XY and is at a distance of 18 cm from A . What will be the length of CD?
View SolutionABandCD are parallel chords of length a cm each.If the shaded area is (2+π)cm2 ,then value of a is
View SolutionIn a circle of radius 5cm, AB and AC are two chords such that AB=AC=8 cm. What is the length of chord BC?
View SolutionIn a circle of radius 5 cm, AB and AC are two chords such that AB=AC=6cm. Find the length of the chord BC
View Solution
