You can keep a book pressed against a wall and prevent it from falling down. Can this horizontal force applied cancel the weight which is a vertical force? Explain.
To understand how a book can be kept pressed against a wall without falling, we need to analyze the forces acting on the book. Here’s a step-by-step solution:
Step 1: Identify the Forces Acting on the Book
When a book is pressed against a wall, there are several forces acting on it:
- Weight (W): This is the downward force due to gravity acting on the book.
- Normal Force (N): This is the force exerted by the wall on the book, acting perpendicular to the wall.
- Frictional Force (f): This is the force that opposes the motion of the book sliding down the wall. It acts upward when the book is pressed against the wall.
Step 2: Apply the Concept of Equilibrium
For the book to remain stationary and not fall, the forces acting on it must be balanced. This means that the upward forces must equal the downward forces.
Step 3: Set Up the Force Balance Equation
In this scenario, the weight of the book (W) acts downward, while the frictional force (f) acts upward. For the book to be in equilibrium:
f=W
This means that the frictional force must be equal to the weight of the book to prevent it from falling.
Step 4: Understand the Role of the Applied Force
When you press the book against the wall, you apply a horizontal force (F). This force causes the wall to exert a normal force (N) on the book. The frictional force is proportional to the normal force:
f=μN
where μ is the coefficient of friction between the book and the wall.
Step 5: Conclusion
Thus, the horizontal force you apply does not directly cancel the weight of the book. Instead, it creates a normal force that increases the frictional force. If the frictional force is sufficient to balance the weight of the book, the book will not fall.
Summary
In conclusion, while the horizontal force applied does not cancel the weight directly, it increases the normal force, which in turn increases the frictional force that can counteract the weight of the book.
---
When a book is pressed against a wall, there are several forces acting on it:
- Weight (W): This is the downward force due to gravity acting on the book.
- Normal Force (N): This is the force exerted by the wall on the book, acting perpendicular to the wall.
- Frictional Force (f): This is the force that opposes the motion of the book sliding down the wall. It acts upward when the book is pressed against the wall.
For the book to remain stationary and not fall, the forces acting on it must be balanced. This means that the upward forces must equal the downward forces.
In this scenario, the weight of the book (W) acts downward, while the frictional force (f) acts upward. For the book to be in equilibrium:
f=W
This means that the frictional force must be equal to the weight of the book to prevent it from falling.
When you press the book against the wall, you apply a horizontal force (F). This force causes the wall to exert a normal force (N) on the book. The frictional force is proportional to the normal force:
f=μN
where μ is the coefficient of friction between the book and the wall.
Thus, the horizontal force you apply does not directly cancel the weight of the book. Instead, it creates a normal force that increases the frictional force. If the frictional force is sufficient to balance the weight of the book, the book will not fall.
In conclusion, while the horizontal force applied does not cancel the weight directly, it increases the normal force, which in turn increases the frictional force that can counteract the weight of the book.
Topper's Solved these Questions
- FRICTIONBook:CENGAGE PHYSICSChapter:FRICTIONExercise:CONSOLIDATED EXERCISE.
Explore 1 Video
- FRICTIONBook:CENGAGE PHYSICSChapter:FRICTIONExercise:CONSOLIDATED EXERCISE. (MULTIPAL-CHOICE QUESTION WITH ONE OR MORE THAN ONE CORRECT ANSWER)
Explore 3 Videos
- FRICTIONBook:CENGAGE PHYSICSChapter:FRICTIONExercise:OLYMPIAD AND NTSE LEVEL EXERCISES (Read the given statements and select the correct option.)
Explore 1 Video
- ELASTICITYBook:CENGAGE PHYSICSChapter:ELASTICITYExercise:OLYMPIAD AND NTSE LEVEL EXERCISES
Explore 10 Videos
- SOUNDBook:CENGAGE PHYSICSChapter:SOUNDExercise:OLYMPIAD AND NTSE LEVEL EXERCISE
Explore 10 Videos
Similar Questions
Can a single force applied to a body change both its translational and rotational motion? Explain.
View SolutionA block of mass m is pressed against a wall which is moving with an acceleration a as shown in figure If the block is pulled at an angle θ with downward vertical by a force F and it does not slide relative to the wall . Find the
a. friction force between the block and wall
b.inimum magnitude of F so as to cayse a relative sliding between the block and wall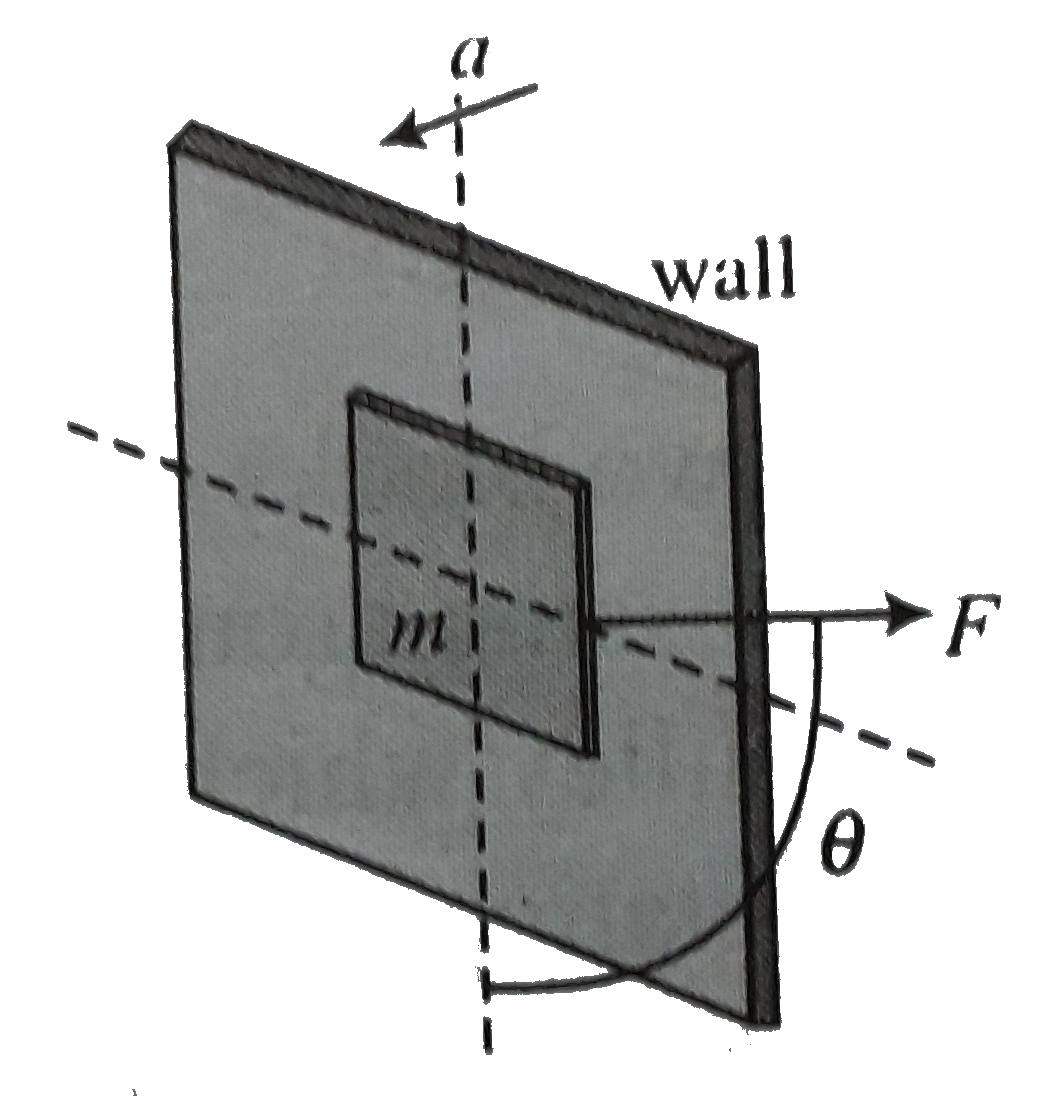
View Solution
Knowledge Check
A block of mass m is held fixed against a wall by a applying a horizontal force F. Which of the following option is incorrect :
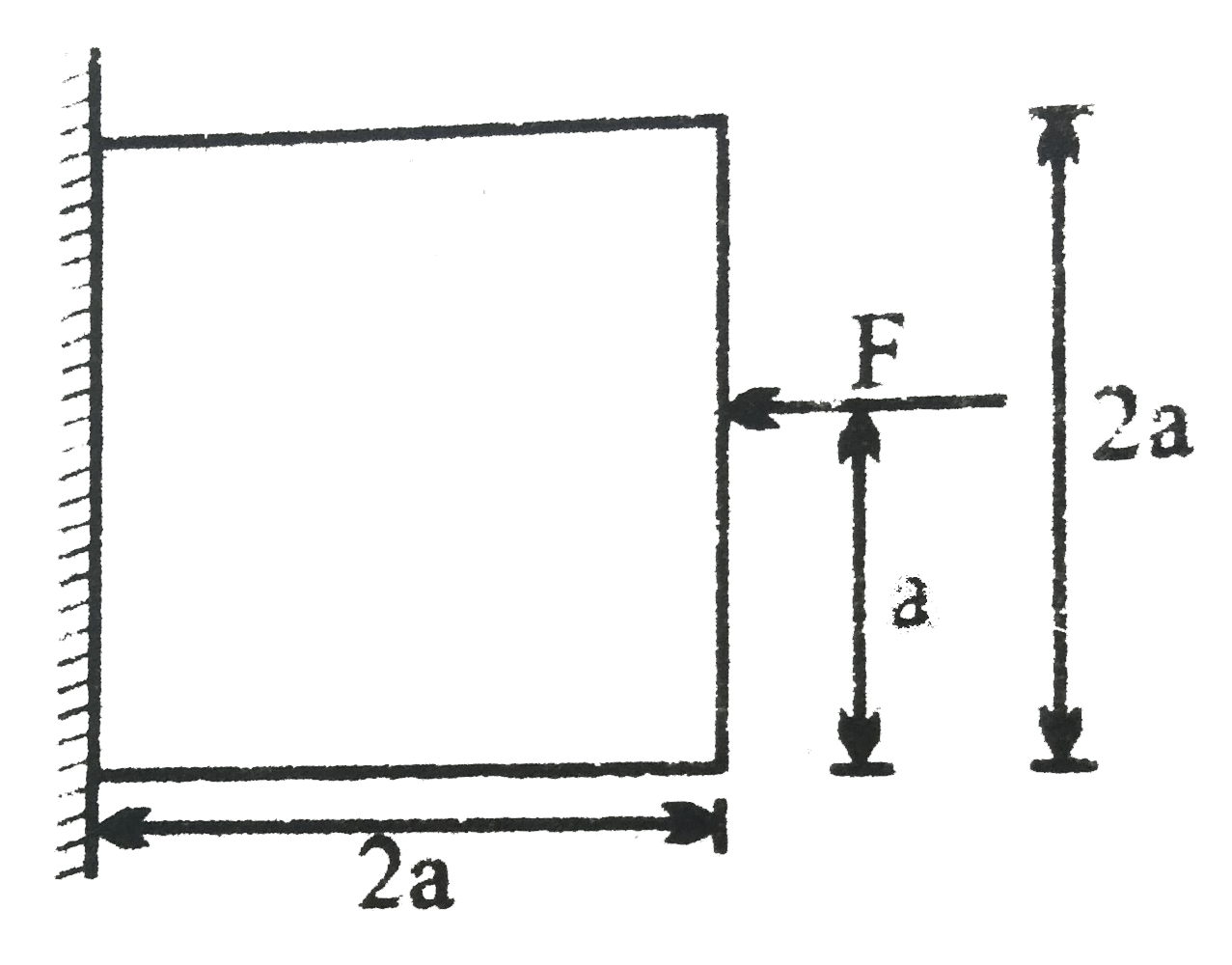 .Afriction force = mgBF will not produce torqueCnormal will not produce torqueDnormal reaction = F
.Afriction force = mgBF will not produce torqueCnormal will not produce torqueDnormal reaction = FTwo blocks A and B of masses 2kg and 8kg respectively are kept in contact and pressed against a roguh vertical wall by applying a horizontal force F=50N as shown, The frictional force acting between the two blocks is
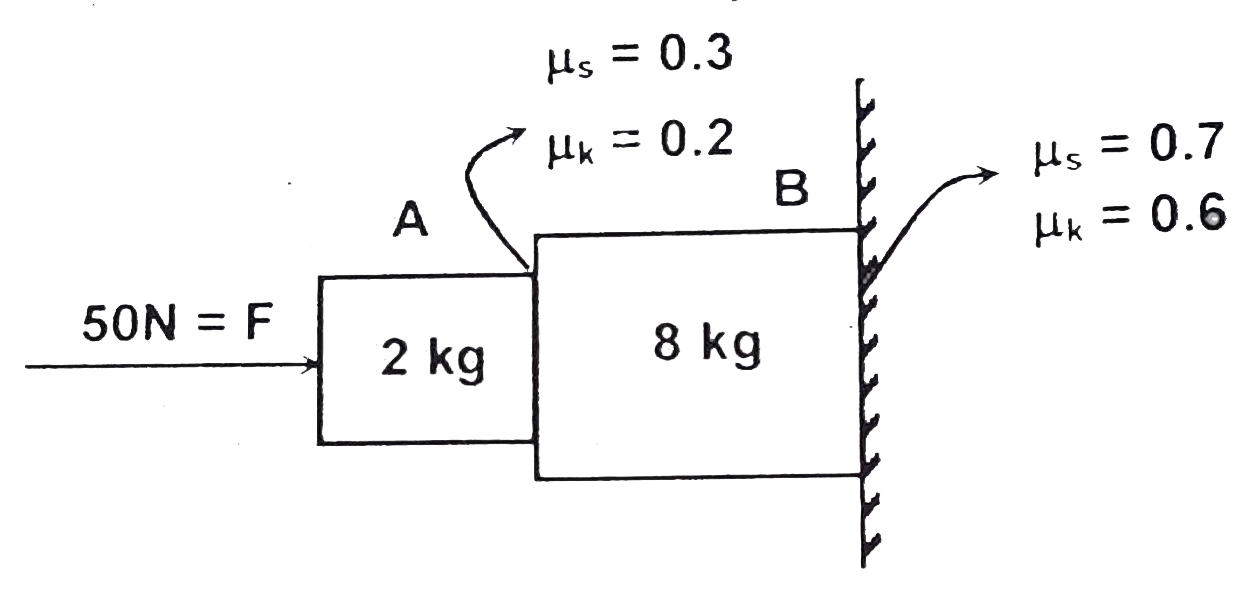 AzeroB6NC8ND10N
AzeroB6NC8ND10N
An object of 2 kg is held pressed, against a vertical wall with the help of a horizontal force (see fig.). The body is about to full down. Which force stopping the object to fall down and what is its magnitude?AStatic friction, 10NBStatic friction, 15NCStatic friction, 20 NDKinetic friction, 20 N
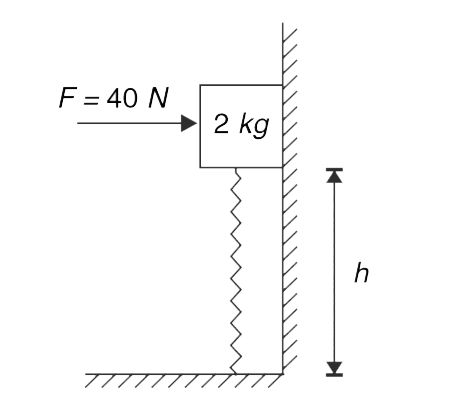
(i) In the arrangement shown in the figure the coefficient of friction between the 2 kg block and the vertical wall is μ=0.5. A constant horizontal force of 40 N keeps the block pressed against the wall. The spring has a natural length of 1.0 m and its force constant is k=400Nm–1. What should be the height h of the block above the horizontal floor for it to be in equilibrium. The spring is not tied to the block.
(ii) A block of mass M is pressed against a rough vertical wall by applying a force F making an angle of θ with horizontal (as shown in figure). Coefficient of friction between the wall and the block is μ=0.75.
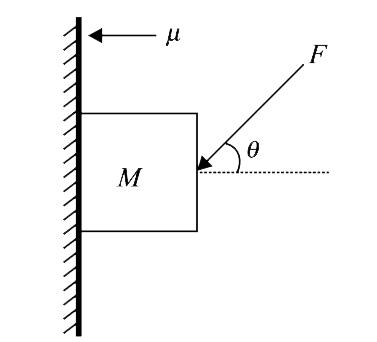
(a) If F = 2 Mg, find the range of values of θ so that the block does not slide
[Take tan37∘=0.75,sin24∘=0.4]
(b) Find the maximum value of θ above which equilibrium is not possible for any magnitude of force F.
View SolutionA block is pressed towards a vertical wall using a horizontal force equal to n times its weight which prevents the block from sliding down.Then coefficient of static friction between the block and the wall is?
View SolutionA block of mass 1kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5 ,magnitude of the frictional force acting on the block is
View SolutionA girl holds a book of mass m against a vertical wall with a horizontal force F using her finger so that the book does not move. The frictional force on the book by the wall is –
View SolutionA girl holds a book of mass m against a vertical wall with a horizontal force F using her finger so that the book does not move. The frictional froce on the book by the wall is :
View Solution

