Question

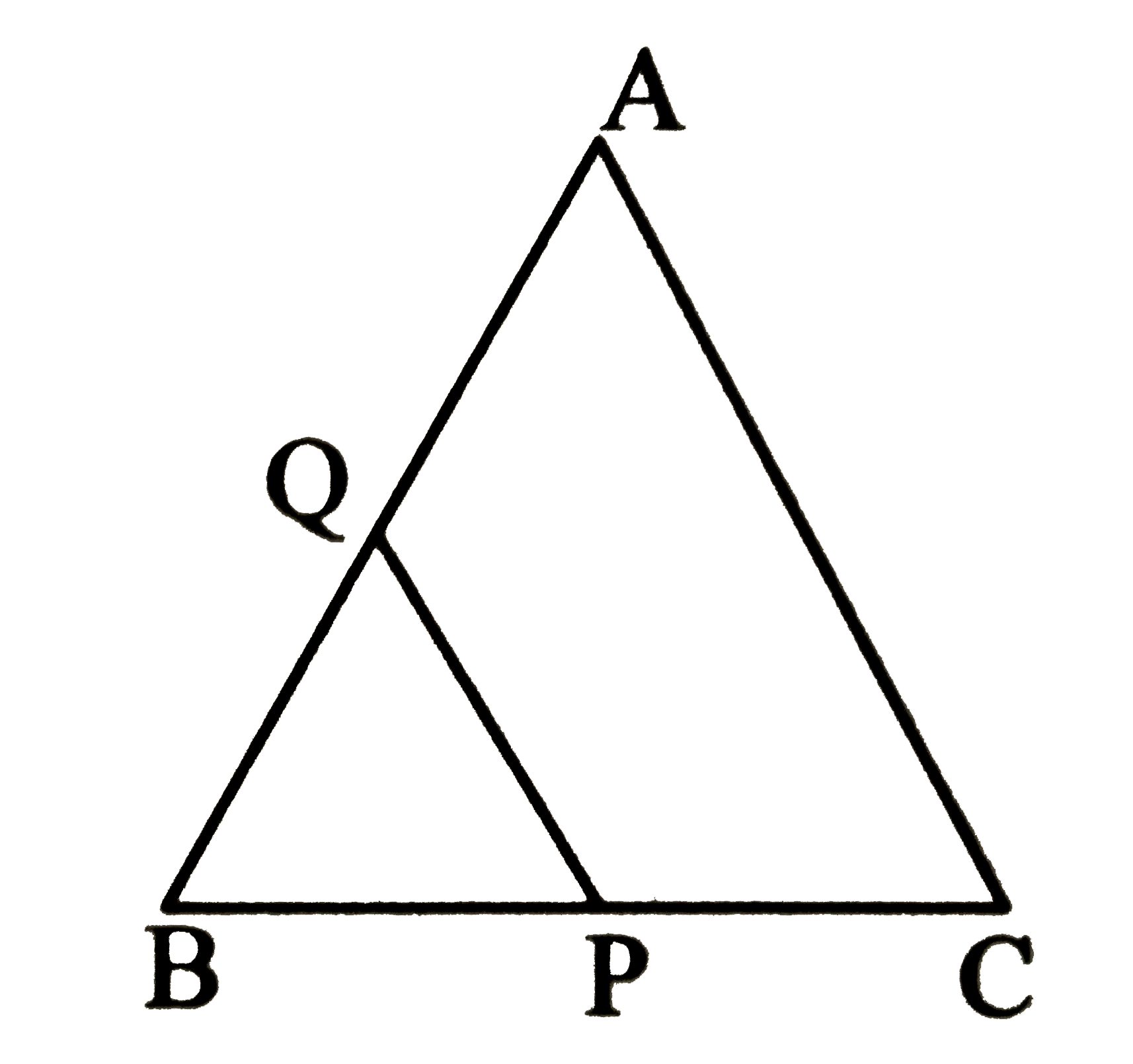
In $\Delta ABC$, P is a point on BC such that BP : PC = 2 : 3 and Q is the midpoint of BP. Then ar $(\Delta ABQ):ar(\Delta ABC)$ is equal to :

Options

A. `1:4`
B. `2:5`
C. `1:5`
D. `2:3`

Answer

C

Explanation

To solve the problem, we need to find the ratio of the area of triangle ABQ to the area of triangle ABC given the conditions about points P and Q.

1. Understand the Ratios: We are given that BP : PC = 2 : 3. This means if we let BP = 2x and PC = 3x, then BC = BP + PC = 2x + 3x = 5x.

2. Assign a Length to BC: For simplicity, let's assume BC = 10 cm. This gives us:
- BP = 2x = 4 cm (since 2/5 of 10 cm is 4 cm)
- PC = 3x = 6 cm (since 3/5 of 10 cm is 6 cm)

3. Identify Point Q: Q is the midpoint of BP. Therefore, the length of BQ = BP/2 = 4 cm / 2 = 2 cm.

4. Area of Triangle ABC: The area of triangle ABC can be calculated using the formula:
\( \text{Area of } \Delta ABC = \frac{1}{2} \times \text{Base} \times \text{Height} = \frac{1}{2} \times BC \times H = \frac{1}{2} \times 10 \times H = 5H \)

5. Area of Triangle ABQ: The area of triangle ABQ can also be calculated using the same formula:
\( \text{Area of } \Delta ABQ = \frac{1}{2} \times BQ \times H = \frac{1}{2} \times 2 \times H = H \)

6. Calculate the Ratio: Now we can find the ratio of the areas:
\( \frac{\text{Area of } \Delta ABQ}{\text{Area of } \Delta ABC} = \frac{H}{5H} = \frac{1}{5} \)

7. Final Result: Therefore, the ratio of the area of triangle ABQ to the area of triangle ABC is:
\( \text{ar}(\Delta ABQ) : \text{ar}(\Delta ABC) = 1 : 5 \)