यदि ΔABC की माध्यिकायें बिंदु G पर प्रतिच्छेद करती है, तो सिद्ध कीजिए कि
ar(ΔAGB)=ar(ΔAGC)=ar(ΔBGC)=13ar(ΔABC)
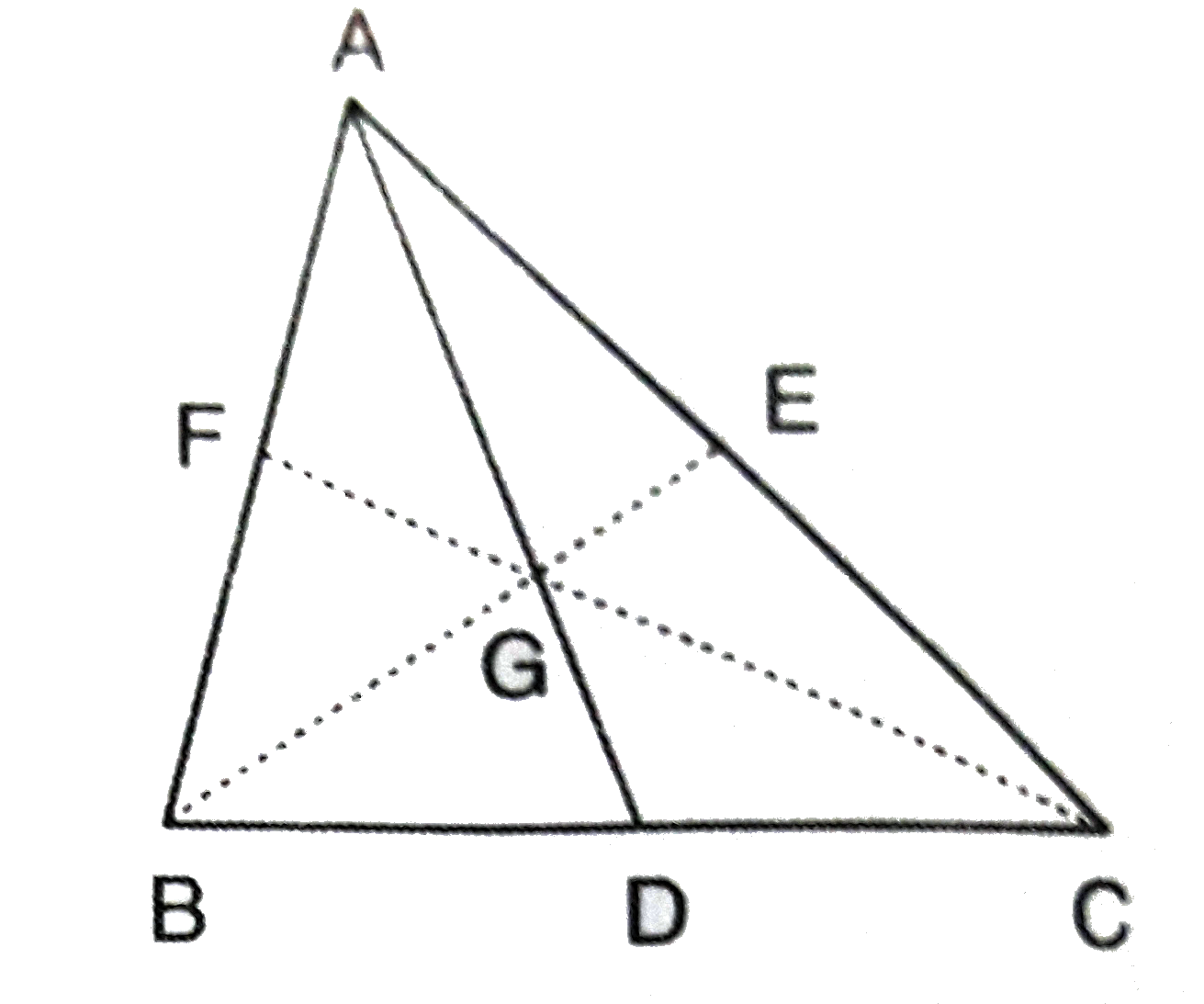
दिया है : एक ΔABC एक प्रकार है कि माध्यिकाये AD , BE तथा CF बिंदु G पर प्रतिच्छेद करती है।
सिद्ध करना है: ar(ΔAGB)=ar(ΔBGC)=ar(CGA)=13ar(ΔABC)
उपपत्ति: हम जानते है कि त्रिभुज की माध्यिका इसे दो समान क्षेत्रफल वाली दो त्रिभुजों में विभाजित करती है।
ΔABC में, AD एक माध्यिका है।
⇒ar(ΔABD)=ar(ΔACD) ... (i)
ΔGBC में, GE एक माध्यिका है।
⇒ar(ΔGBD)=ar(ΔGCD) ...(ii)
(i ) में से (ii ) के संगत पक्षों को घटाने पर,
ar(ΔABD)−ar(ΔGBD)=ar(ΔACD)−ar(ΔGCD)
∴ar(ΔAGB)=ar(ΔAGC) ...(iii)
इसी प्रकार,
ar(ΔAGB)=ar(ΔBGC) ...(iv)
(iii ) तथा (iv) से
ar(ΔAGB)=ar(ΔBGC)=ar(ΔAGC) ...(v)
परन्तु ar(ΔAGB)+ar(ΔBGC)+ar(ΔAGC)=ar(ΔABC)
∴3ar(ΔAGB)=ar(ΔABC)
⇒ar(ΔAGB)=13ar(ΔABC)
अतः ar(ΔAGB)=ar(ΔAGC)=ar(ΔBGC)=13ar(ΔABC)
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:व्याख्यात्मक उदाहरण
Explore 1 Video
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:प्रश्नावली 15.1
Explore 6 Videos
- संख्यिकीय आंकड़ों का आलेखीय निरूपण Book:RD SHARMAChapter:संख्यिकीय आंकड़ों का आलेखीय निरूपण Exercise:बहु विकल्पीय प्रश्न
Explore 8 Videos
- सर्वांगसम त्रिभुजेंBook:RD SHARMAChapter:सर्वांगसम त्रिभुजेंExercise:बहु विकल्पीय प्रश्न
Explore 17 Videos
Similar Questions
चित्र में , P समान्तर चतुर्भुज ABCD के अभ्यन्तर में स्थित कोई बिंदु है दर्शाइए कि
(i) ar(ΔAPB)+ar(ΔPCD)=12ar(।।gmABCD)
(ii) ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)

View Solutionआकृति में आकृति एक ही आधार तथा समान समांतर रेखाओं के बीच स्थित है :

View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
View SolutionIf ΔABC~ΔQRP,ar(ΔABC)ar(ΔPQR)=94, AB=18 cm and BC=15 cm, then PR is equal to
View SolutionIn the figure, ABC and BDE are two equilateral triangle such that D is the mid-point of BC. If AE intersects BC at F, show that:
(i) ar(ΔBDE)=14ar(ΔABC) (ii) ar(ΔBDE)=12ar(ΔBAE)
(iii) ar(ΔABC)=2ar(ΔBEC) (iv) ar(ΔBFE)=ar(ΔAFD)
(v) ar(ΔBFE)=2ar(ΔFED) (vi) ar(ΔFED)=18ar(ΔAFC)

View Solutionयदि ABCD एक समांतर चतुर्भुज है, तो सिद्ध कीजिए कि
ar(ΔABD)=ar(ΔBCD)=ar(ΔABC)=ar(ΔACD)=12ar(||gmABCD)
View SolutionΔABC में, भुजाओं AB तथा BC के मध्य-बिंदु क्रमशः P तथा Q है और AP का मध्य-बिंदु R है। सिद्ध कीजिए कि
(i)ar(ΔPBQ)=ar(ΔARC) (ii)ar(ΔPRQ)=12ar(ΔARC)
(iii)ar(ΔRQC)=38ar(ΔABC)
View Solutionत्रिभुज ABC की AD एक माध्यिका है तथा भुजा AC पर बिंदु P इस प्रकार है कि
ar(ΔADP):ar(ΔABD)=2:3, तो ar(ΔPDC):ar(ΔABC)
View Solutionयदि ΔABC~ΔPQR तथा BC=5QR तो ar(ΔABC):ar(ΔPQR) है
View SolutionΔABC का आधार BC बिन्दु D से इस प्रकार विभाजित होता है कि BD=12DC है। सिद्ध कीजिए कि ar(ΔABD)=13ar(ΔABC).
View SolutionFrom the given figure, ar ( DeltaADE ): ar ( DeltaABC )= …………..
View SolutionΔABC~ΔPQR, AB:PQ=3:4 then ar ΔABC: ar ΔPQR=……
View SolutionΔABC~ΔDEF if DE:AB=2:3 and arΔDEF=44sq. Units then arΔABC= ……………sq. units.
View Solutionकिसी त्रिभुज ABC की माध्यिकाएँ AD, BE, CF बिन्दु G पर मिलती हैं | दर्शाइए कि :
ΔAGB=ΔBGC=ΔCGA=13ΔABC.
View Solution

