त्रिज्या R के एक विषमांगी गोले में निम्न घनत्व भिन्नताएँ हैं-
ρ=ρ0,r≤R3
=12ρ0,R3<r≤3R4
=18ρ0,3R4<r≤R
गोले के केन्द्र से 2R दूरी पर गुरुत्वीय क्षेत्र क्या होगा?
0.1πGRρ0
0.2πGRρ0
0.3πGRρ0
0.4πGRρ0
The correct Answer is:A
गोले के केन्द्र से 20 दूरी पर गुरुत्वीय क्षेत्र
E=GM(2R)2
जहाँ, M = सम्पूर्ण गोले का द्रव्यमान है।

यहाँ M=43π(R3)2ρ0+{43π(34R)3−43π(R3)3}
ρ02+{43πR3−43π(34R)3}ρ−08
=43πR3ρ0{127+728−154+18−27512}
=43πR3ρ0{52+2916−256+1728−72913824}
=43πR3ρ0{5156−98513824}
=43πR3ρ0{417113824}
=0.402πR3ρ0
∴E=G(0.402πR3ρ0)(2R)2=0.1πGRρ0
Similar Questions
निम्नलिखित को अंतराल में लिखिए:
(i) {x:x∈R,−4<x≤6}
(ii) {x:x∈R,−12<x<−10}
(iii) {x:x∈R,0≤x<7}
(iv) {x:x∈R,3≤x≤4}
View Solutionत्रिज्या R के एक विषमांगी गोले में निम्न घनत्व भिन्नताएँ हैं-
ρ=ρ0,r≤R3
=12ρ0,R3<r≤3R4
=18ρ0,3R4<r≤R
गोले के केन्द्र से 2R दूरी पर गुरुत्वीय क्षेत्र क्या होगा?
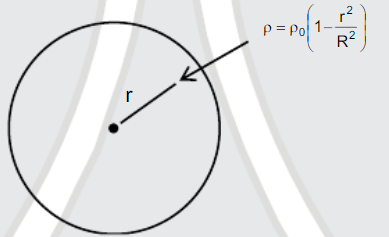
View SolutionMass density of sphere having radius R varies as ρ=ρ0(1−r2R2) . Find maxium magnitude of gravitational field
View SolutionCharge density of a sphere of radius R is rho = rho_0/r where r is distance from centre of sphere.Total charge of sphere will be
View SolutionA non-homogeneous sphere of radius R has the following density variation : rho{{:(rho_(0),rleR//3),(rho_(0)//2,(R//3) lt r le (3R//4)),(rho_(0)//8,(3R//4) lt r le R):} The gravitational field at a distance 2R from the centre of the sphere is
View Solutionएक असमरूप लेकिन गोलिय समरूप आवेशो का वितरण का आवेश घनत्व ρ है जो कि
ρ=ρ0(1−r/R) r≤R, के लिए
ρ=0 r≥R, के लिए
जहाँ ρ0=3Q/πR3 नियत है।
(a) क्षेत्र r < R के लिये विद्युत क्षेत्र का व्यंजक प्राप्त करें।
(b) गोले में स्थित कुल आवेश ज्ञात कीजिये।
View SolutionFor 4 ≤r≤n
(nr)+4(nr+1)+6(nr+2)=4(nr+3)+(nr+4) equals
View SolutionA spherically symmetric charge distribution is characterized by a charge density having the following variation : rho (r ) = rho_0 (1 - r/R) for r lt R rho (r ) = 0 for r ge R . Where r is the distance from the centre of the charge distribution and rho_0 is a constant. The electric field at an internal point (r lt R) is
View Solution
