संलग्न चित्र में नाभिकों को प्रति न्यूक्लिऑन बन्धन ऊर्जा Eb तथा द्रव्यमान संख्या M के बीच ग्राफ खींचा गया है. A,B,C,D.E,F विभिन नाभिकों को दर्शाते हैं. चार प्रक्रियाएं लेने पर
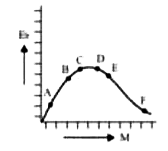
(i) A+B→C+e (ii) C→A+B+e
(iii) D+E=F+∈ (iv) F→D+E+∈
जहाँ ∈ मुक्त ऊर्जा है. किस प्रक्रिया में ∈ धनात्मक है?
(i) तथा (iv)
(i) तथा (iii)
(ii) तथा (iv)
(ii) तथा (iii)
The correct Answer is:A
भारी नाभिक के हल्के नाभिकों में टूटने पर ऊर्जा मुक्त होती है एवं जब हल्के नाभिक संयुक्त होकर भारी नाभिक बनाते है, तब भी ऊर्जा मुक्त होती है.
Similar Questions
In Figure, DE∣∣AC and DF∣∣AE . Prove that EFBF=ECBE .
View SolutionIn Figure, CD and GH are respectively the medians of ABC and EFG . If ABC~FEG , prove that (i)ADC~FHG (ii)CDGH=ABFE (iii)CDB~GHE
View SolutionIn Figure, DEFG is a square and ∠BAC=90 . Prove that (i) A G F ~ D B G(ii)AGF~EFC (iii) D B G ~ E F C(iv)DE2=BDxEC
View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=34 , then write Area (ABC):Area(DEF) .
View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=25 , then Area(ABC):Area(DEF)=
View SolutionIf in two triangles ABC and DEF , ABDE=BCFE=CAFD , then FDECAB (b) FDEABC (c) CBAFDE (d) BCAFDE
View SolutionIn Figure, the incircle of ABC touches the sides BC, CA and AB at D, E and F respectively. Show that AF+BD+CE=AE+BF+CD=12(Perimeter of ABC).
View SolutionD, E, F are the mid-point of the sides BC, CA and AB respectively of △ABC. Then DEF is congruent to triangle.
(a)ABC
(b) AEF
(c) BFD, CDE
(d) AFE, BFD, CDE
View Solution