In ΔABC,∠B=90∘,AC=29cmandBC=20cm. Then 1−sinA+cosA1+sinA+cosA is equal to :
A)38
B)37
C)12
D)14
The correct Answer is:B
To solve the problem, we need to find the value of the expression (1−sinA+cosA)/(1+sinA+cosA) in triangle ABC where ∠B=90∘, AC=29cm, and BC=20cm.
1. Identify the sides of the triangle:
- Given that AC is the hypotenuse (29 cm) and BC is one of the legs (20 cm), we need to find the length of the other leg AB.
2. Use the Pythagorean theorem:
- According to the Pythagorean theorem, AC2=AB2+BC2.
- Plugging in the values:
292=AB2+202
841=AB2+400
AB2=841−400=441
AB=√441=21cm
3. Find sinA and cosA:
- In triangle ABC:
- sinA=oppositehypotenuse=BCAC=2029
- cosA=adjacenthypotenuse=ABAC=2129
4. Substitute sinA and cosA into the expression:
- We need to calculate:
1−sinA+cosA1+sinA+cosA
- Substitute the values:
1−2029+21291+2029+2129
5. Simplify the numerator and denominator:
- For the numerator:
1−2029+2129=2929−2029+2129=29−20+2129=3029
- For the denominator:
1+2029+2129=2929+2029+2129=29+20+2129=7029
6. Final calculation:
- Now, we can simplify the entire expression:
30297029=3070=37
Conclusion:
The value of 1−sinA+cosA1+sinA+cosA is 37.
- Given that AC is the hypotenuse (29 cm) and BC is one of the legs (20 cm), we need to find the length of the other leg AB.
- According to the Pythagorean theorem, AC2=AB2+BC2.
- Plugging in the values:
292=AB2+202
841=AB2+400
AB2=841−400=441
AB=√441=21cm
- In triangle ABC:
- sinA=oppositehypotenuse=BCAC=2029
- cosA=adjacenthypotenuse=ABAC=2129
- We need to calculate:
1−sinA+cosA1+sinA+cosA
- Substitute the values:
1−2029+21291+2029+2129
- For the numerator:
1−2029+2129=2929−2029+2129=29−20+2129=3029
- For the denominator:
1+2029+2129=2929+2029+2129=29+20+2129=7029
- Now, we can simplify the entire expression:
30297029=3070=37
The value of 1−sinA+cosA1+sinA+cosA is 37.
Topper's Solved these Questions
- SSC SELECTION POST 10 NOV 2020 SHIFT 2 HSC LEVELBook:SSC SELECTION POSTChapter:SSC SELECTION POST 10 NOV 2020 SHIFT 2 HSC LEVELExercise:QUANTITATIVE APTITUDE
Explore 25 Videos
- SSC SELECTION POST 14 DEC 2020 SHIFT 3 GRADUATION POST Book:SSC SELECTION POSTChapter:SSC SELECTION POST 14 DEC 2020 SHIFT 3 GRADUATION POST Exercise:QUANTITATIVE APTITUDE
Explore 25 Videos
Similar Questions
Knowledge Check
In △ABC, ∠B=90∘ , AB=5cm and AC=13cm. Then, BC = ?
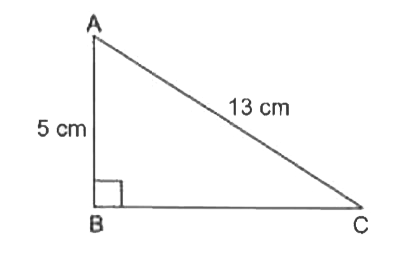 A8 cmB18 cmC12 cmDnone of these
A8 cmB18 cmC12 cmDnone of theseIn ΔABC, AB=6√3cm, AC=12cm and BC=6cm. Then ∠B is
A45∘B60∘C90∘D120∘In ΔABC,∠B=90∘ and BD⊥AC. If AC = 9 cm and AD = 3 cm, then BD is equal to :
A2√2 cmB3√2 cmC2√3 cmD3√3 cm
In a ΔABC,∠B=90∘,AB=7cmand(AC−BC)=1cm, find the values of sinA,cosA,sinCandC.
View SolutionIn ΔABC,∠B=90∘andBD⊥AC.IfAC=9cmandAD=3 cm then BD is equal to
View SolutionIn a ΔABC,∠B=90∘,AB=5cmand(BC+AC)=25cm. Find the values of sinA,cosA,cosec AandsecA.
View SolutionIn a ΔABC,∠B=90∘,AB=12cmandBC=5cm
find (i)cosA
(ii)cosecA
(iii)cosC
(iv)cosecC.
View SolutionIf ΔABC right angle at B, BC = 5 cm and AC -AB =1 cm. then 1+sinCcosC is equal to
View Solution
