In a parallelogram OABC vectors a,b,c respectively, THE POSITION VECTORS OF VERTICES A,B,C with reference to O as origin. A point E is taken on the side BC which divides it in the ratio of 2:1 also, the line segment AE intersects the line bisecting the angle ∠AOC internally at point P. if CP when extended meets AB in points F, then
Q. The position vector of point P isSolution in Kannada
2|a|||a|−3|c∣∣
|a|||a|−3|c∣∣
3|a|||a|−3|c∣∣
3|c|3||c|−|a∣∣
The correct Answer is:B
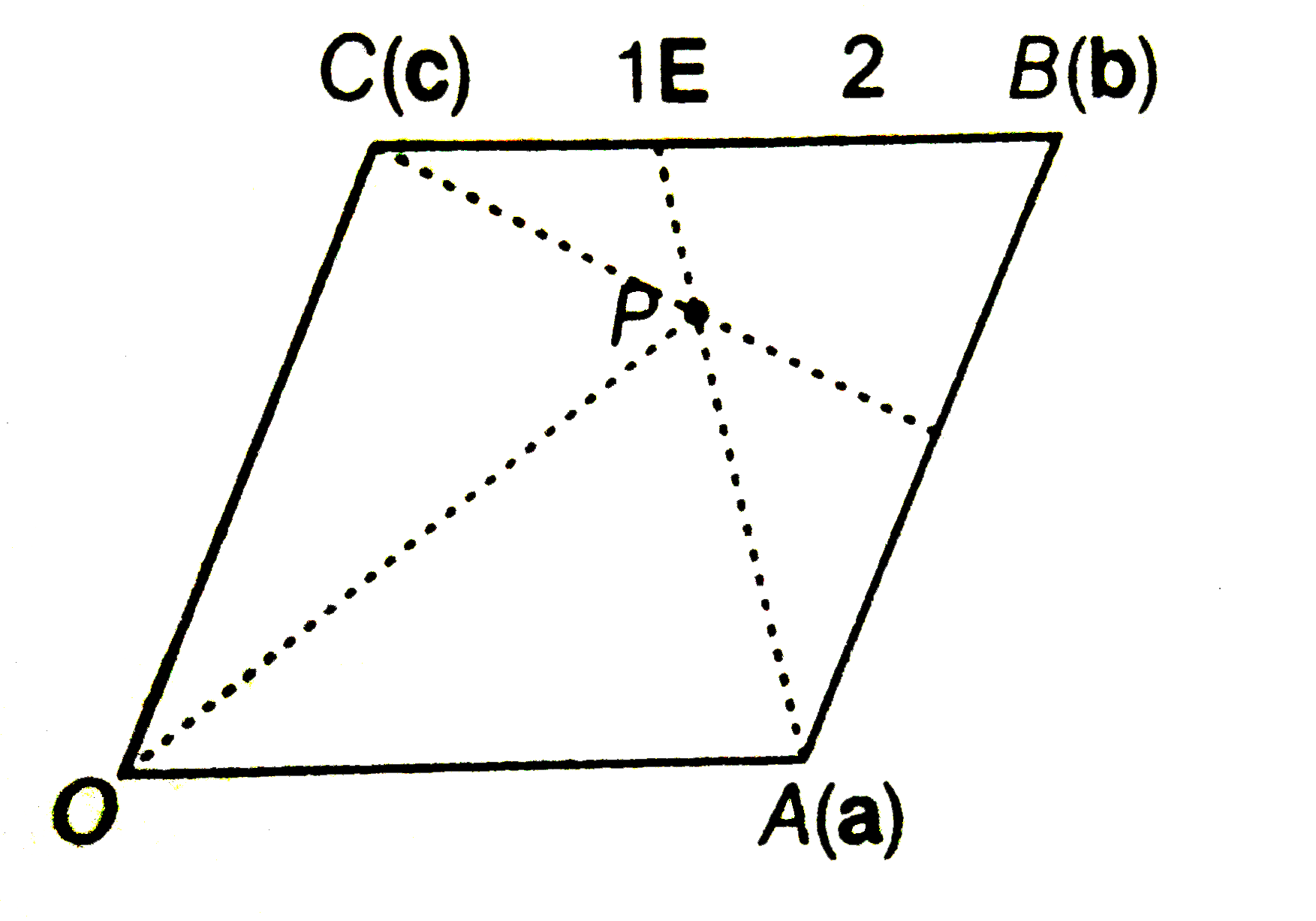
let the position vector fo A and C be a and c respectively.
therefore,
Position vector of
B=b=a+c . . (i)
Also, position vector of
E=b+2c3=a+3c3 . . . (ii)
Now, point P lies on angle bisector off ∠AOC. thus,
Position vector of point
P=λ(a|a|+b|b|) . . (iii)
Also, let P divides EA in ration μ:1. therefore, position vector of P
=μa+a+3c3μ+1=(3μ+1)a+3c3(μ+1) . . . (iv)
Comparing eqs. (iii) and (iv), we get
λ(a|a|+c|c|)=(3μ+1)a+3c3(μ+1)
⇒λ|a|=3μ+13(μ+1)andλ|c|=1μ+1
⇒3|c|−|a|3|a|=μ
⇒λ|c|=13|c|−|a|3|a|+1⇒λ=3|a||c|∣3|c|+2|a|
Let F divides AB in ratio t:1, then position vector of F is
tb+at+1
Now, points C, P,F are collinear, then, CF=mCP
⇒t(a+c)t+1−c=m{3|a||c|3|c|+2|a|(a|a|+c|c|)−c}
Comparing coefficient, we get
tt+1=m3|c|3|c|+2|a|
and −1t+1=m|a|−3|c|3|c|+2|a|
t=3|c|3|c|−|a|
Similar Questions
In a parallelogram OABC, vectors →a,→b,→c are respectively the positions of vectors of vertices A,B,C with reference to O as origin. A point E is taken on the side BC which divide the line 2:1 internally. Also the line segment AE intersect the line bisecting the angle O internally in point P. If CP, when extended meets AB in point F. Then The position vector of point P, is
View SolutionIn a parallelogram OABC, vectors veca, vecb, vecc are, respectively, tehe position vectors of vertices A, B, C with reference to O as origin. A point E is taken on the side BC which divides it in the ratio 2 : 1 . Also, the line segment AE intersects the line bisecting the angle angle AOC internally at point P. If CP when extended meets AB in point F, then The position vector of point P is
View SolutionIn a parallelogram OABC, vectors veca, vecb, vecc are, respectively, tehe position vectors of vertices A, B, C with reference to O as origin. A point E is taken on the side BC which divides it in the ratio 2 : 1 . Also, the line segment AE intersects the line bisecting the angle angle AOC internally at point P. If CP when extended meets AB in point F, then The ratio in which F divides AB is
View SolutionIn a parallelogram OABC, vectors →a,→b,→c are respectively the positions of vectors of vertices A,B,C with reference to O as origin. A point E is taken on the side BC which divide the line 2:1 internally. Also the line segment AE intersect the line bisecting the angle O internally in point P. If CP, when extended meets AB in point F. Then The position vector of point P, is
View SolutionIn a parallelogram OABC vectors a,b,c respectively, THE POSITION VECTORS OF VERTICES A,B,C with reference to O as origin. A point E is taken on the side BC which divides it in the ratio of 2:1 also, the line segment AE intersects the line bisecting the angle ∠AOC internally at point P. if CP when extended meets AB in points F, then
Q. The ratio in which F divides AB is
View SolutionIf a and b are position vector of two points A,B and C divides AB in ratio 2:1 internally, then position vector of C is
View SolutionIn a parallelogram OABC with position vectors of A is 3hat(i)+4hat(j) and C is 4hat(i)+3hat(j) with reference to O as origin. A point E is taken on the side BC which divides it in the the ratio of 2:1 . Also, the line segment AE intersects the line bisecting the angleAOC internally at P. CP when extended meets AB at F. Q. The position vector of P is
View SolutionIn a parallelogram OABC with position vectors of A is 3hat(i)+4hat(j) and C is 4hat(i)+3hat(j) with reference to O as origin. A point E is taken on the side BC which divides it in the the ratio of 2:1 . Also, the line segment AE intersects the line bisecting the angleAOC internally at P. CP when extended meets AB at F. Q. The equation of line parallel of CP and passing through (2, 3, 4) is
View Solution
