In a parallelogram OABC vectors a,b,c respectively, THE POSITION VECTORS OF VERTICES A,B,C with reference to O as origin. A point E is taken on the side BC which divides it in the ratio of 2:1 also, the line segment AE intersects the line bisecting the angle $∠ A O C$ internally at point P. if CP when extended meets AB in points F, then
Q. The ratio in which F divides AB is

$\frac{2 | a |}{| | a | - 3 | c ∣ ∣}$

$\frac{| a |}{| | a | - 3 | c ∣ ∣}$

$\frac{3 | a |}{| | a | - 3 | c ∣ ∣}$

$\frac{3 | c |}{3 | | c | - | a ∣ ∣}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

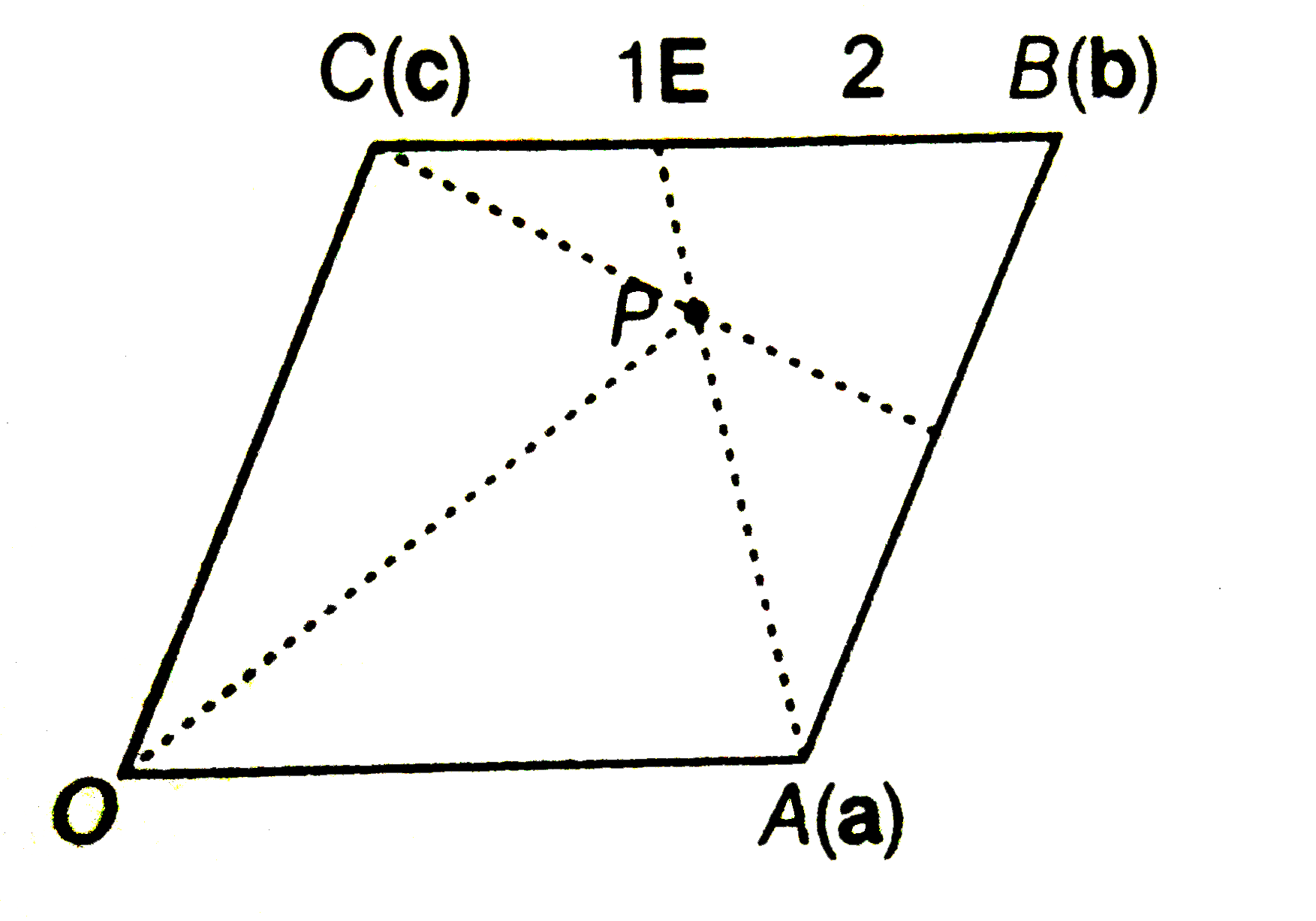
let the position vector fo A and C be a and c respectively.
therefore,
Position vector of
$B = b = a + c$ . . (i)
Also, position vector of
$E = \frac{b + 2 c}{3} = \frac{a + 3 c}{3}$ . . . (ii)
Now, point P lies on angle bisector off $∠ A O C$ . thus,
Position vector of point
$P = λ (\frac{a}{| a |} + \frac{b}{| b |})$ . . (iii)
Also, let P divides EA in ration $μ : 1$ . therefore, position vector of P
$= \frac{μ a + \frac{a + 3 c}{3}}{μ + 1} = \frac{(3 μ + 1) a + 3 c}{3 (μ + 1)}$ . . . (iv)
Comparing eqs. (iii) and (iv), we get
$λ (\frac{a}{| a |} + \frac{c}{| c |}) = \frac{(3 μ + 1) a + 3 c}{3 (μ + 1)}$
$\Rightarrow \frac{λ}{| a |} = \frac{3 μ + 1}{3 (μ + 1)} and \frac{λ}{| c |} = \frac{1}{μ + 1}$
$\Rightarrow \frac{3 | c | - | a |}{3 | a |} = μ$
$\Rightarrow \frac{λ}{| c |} = \frac{1}{\frac{3 | c | - | a |}{3 | a |} + 1} \Rightarrow λ = \frac{3 | a | | c | ∣}{3 | c | + 2 | a |}$
Let F divides AB in ratio t:1, then position vector of F is
$\frac{t b + a}{t + 1}$
Now, points C, P,F are collinear, then, CF=mCP
$\Rightarrow \frac{t (a + c)}{t + 1} - c = m {\frac{3 | a | | c |}{3 | c | + 2 | a |} (\frac{a}{| a |} + \frac{c}{| c |}) - c}$
Comparing coefficient, we get
$\frac{t}{t + 1} = m \frac{3 | c |}{3 | c | + 2 | a |}$
and $\frac{- 1}{t + 1} = m \frac{| a | - 3 | c |}{3 | c | + 2 | a |}$
$t = \frac{3 | c |}{3 | c | - | a |}$

Updated on:21/07/2023

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

Knowledge Check

In a parallelogram OABC, vectors $\to a, \to b, \to c$ are, respectively, tehe position vectors of vertices A, B, C with reference to O as origin. A point E is taken on the side BC which divides it in the ratio $2 : 1$ . Also, the line segment AE intersects the line bisecting the angle $∠ A O C$ internally at point P. If CP when extended meets AB in point F, then
The ratio in which F divides AB is
A $\frac{2 | \to a |}{| | \to a - 3 | \to c | ∣}$
B $\frac{| \to a |}{| | \to a | - 3 | \to c ∣ ∣}$
C $\frac{3 | \to a |}{| | \to a | - 3 | \to c ∣ ∣}$
D $\frac{3 | \to c |}{3 | \to c | - | \to a |}$
In a parallelogram OABC, vectors $\to a, \to b, \to c$ are, respectively, tehe position vectors of vertices A, B, C with reference to O as origin. A point E is taken on the side BC which divides it in the ratio $2 : 1$ . Also, the line segment AE intersects the line bisecting the angle $∠ A O C$ internally at point P. If CP when extended meets AB in point F, then
The position vector of point P is
A $\frac{| \to a | | \to c |}{3 | \to c | + 2 | \to a |} (\frac{\to a}{| \to a |} + \frac{\to c}{| \to c |})$
B $\frac{3 | \to a | | \to c |}{3 | \to c | + 2 | \to a |} (\frac{\to a}{| \to a |} + \frac{\to c}{| \to c |})$
C $\frac{2 | \to a | | \to c |}{3 | \to c | + 2 | \to a |} (\frac{\to a}{| \to a |} + \frac{\to c}{| \to c |})$
DNone of these
In a parallelogram OABC with position vectors of A is $3 ˆ i + 4 ˆ j and C i s 4 ˆ i + 3 ˆ j$ with reference to O as origin. A point E is taken on the side BC which divides it in the the ratio of $2 : 1$ . Also, the line segment AE intersects the line bisecting the $∠ A O C$ internally at P. CP when extended meets AB at F.
Q. The position vector of P is
A $ˆ i + ˆ j$
B $\frac{2}{3} (ˆ i + ˆ j)$
C $\frac{13}{3} (ˆ i + ˆ j)$
D $\frac{21}{5} (ˆ i + ˆ j)$

ARIHANT MATHS-VECTOR ALGEBRA-Exercise (Questions Asked In Previous 13 Years Exam)

Home
Ask Doubt
Profile

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

ARIHANT MATHS-VECTOR ALGEBRA-Exercise (Questions Asked In Previous 13 Years Exam)