Question

In a parallelogram $OABC,$ vectors $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ are respectively the positions of vectors of vertices $A,B,C$ with reference to O as origin. A point E is taken on the side BC which divide the line $2:1$ internally. Also the line segment AE intersect the line bisecting the angle O internally in point P. If CP, when extended meets AB in point F. Then The position vector of point P, is

Options

C. `

Answer

B

Explanation

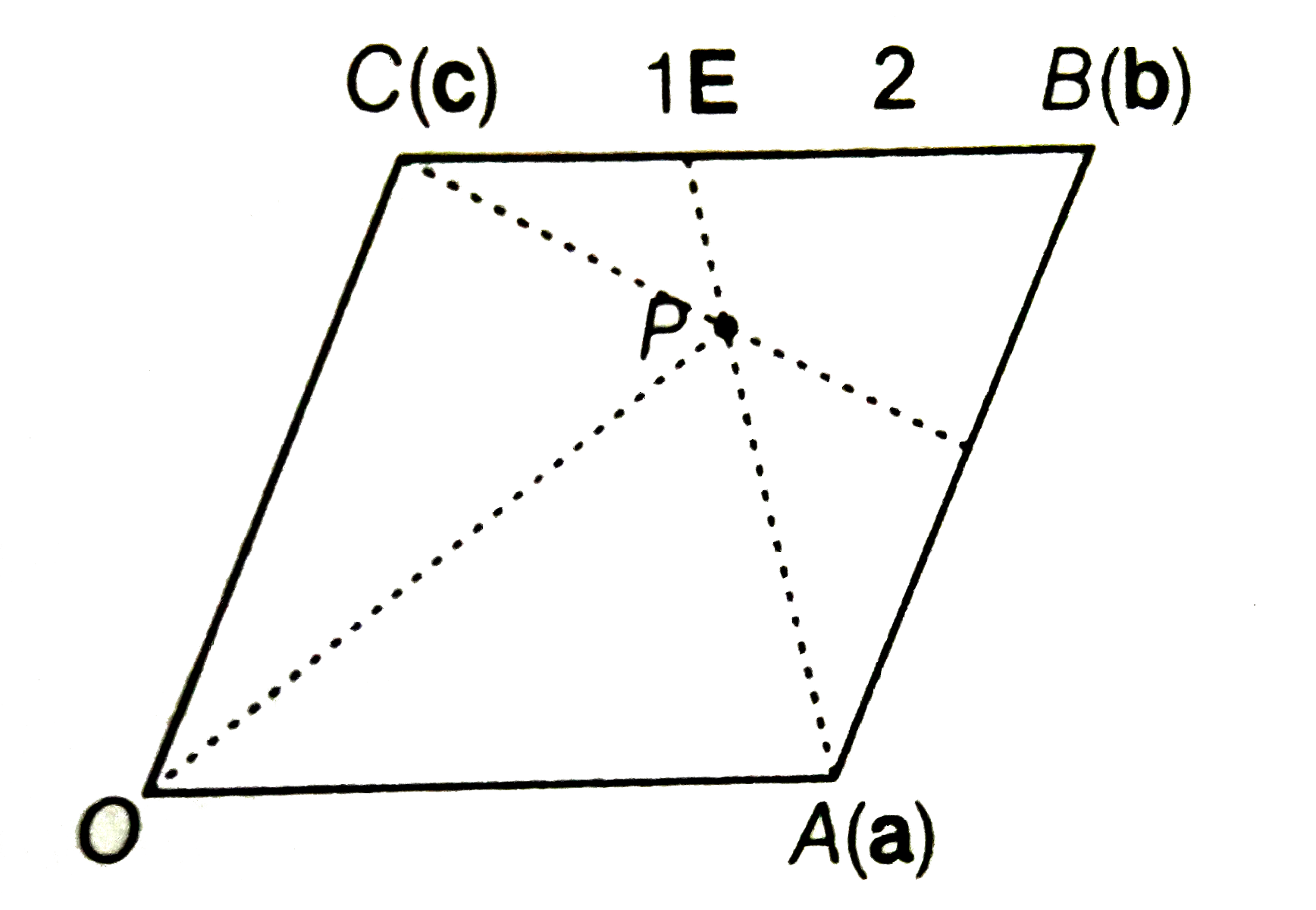
let the position vector fo A and C be a and c respectively.
therefore,
Position vector of
`B=b=a+c` . . (i)
Also, position vector of
`E=(b+2c)/(3)=(a+3c)/(3)` . . . (ii)
Now, point P lies on angle bisector off `angleAOC`. thus,
Position vector of point
`P=lamda((a)/(|a|)+(b)/(|b|))` . . (iii)
Also, let P divides EA in ration `mu:1`. therefore, position vector of P
`=(mua+(a+3c)/(3))/(mu+1)=((3mu+1)a+3c)/(3(mu+1))` . . . (iv)
Comparing eqs. (iii) and (iv), we get
`lamda((a)/(|a|)+(c)/(|c|))=((3mu+1)a+3c)/(3(mu+1))`
`implies(lamda)/(|a|)=(3mu+1)/(3(mu+1)) and (lamda)/(|c|)=(1)/(mu+1)`
`implies(3|c|-|a|)/(3|a|)=mu`
`implies(lamda)/(|c|)=(1)/((3|c|-|a|)/(3|a|)+1)implies lamda=(3|a||c||)/(3|c|+2|a|)`
so, position vector off `P` is `(3|a||c|)/(3|c|+2|a|)((a)/(|a|)+(c)/(|c|))`.