If both the roots of the quadratic equation x2−2kx+(k2+k−5)=0 are less than 5, then k lies in the interval Solution in Kannada
(−∞,4)
[4,5]
(5,6)
(6,∞)
The correct Answer is:A
Let f(x)=x2−2kx+k2+k then α
Consider the following cases:
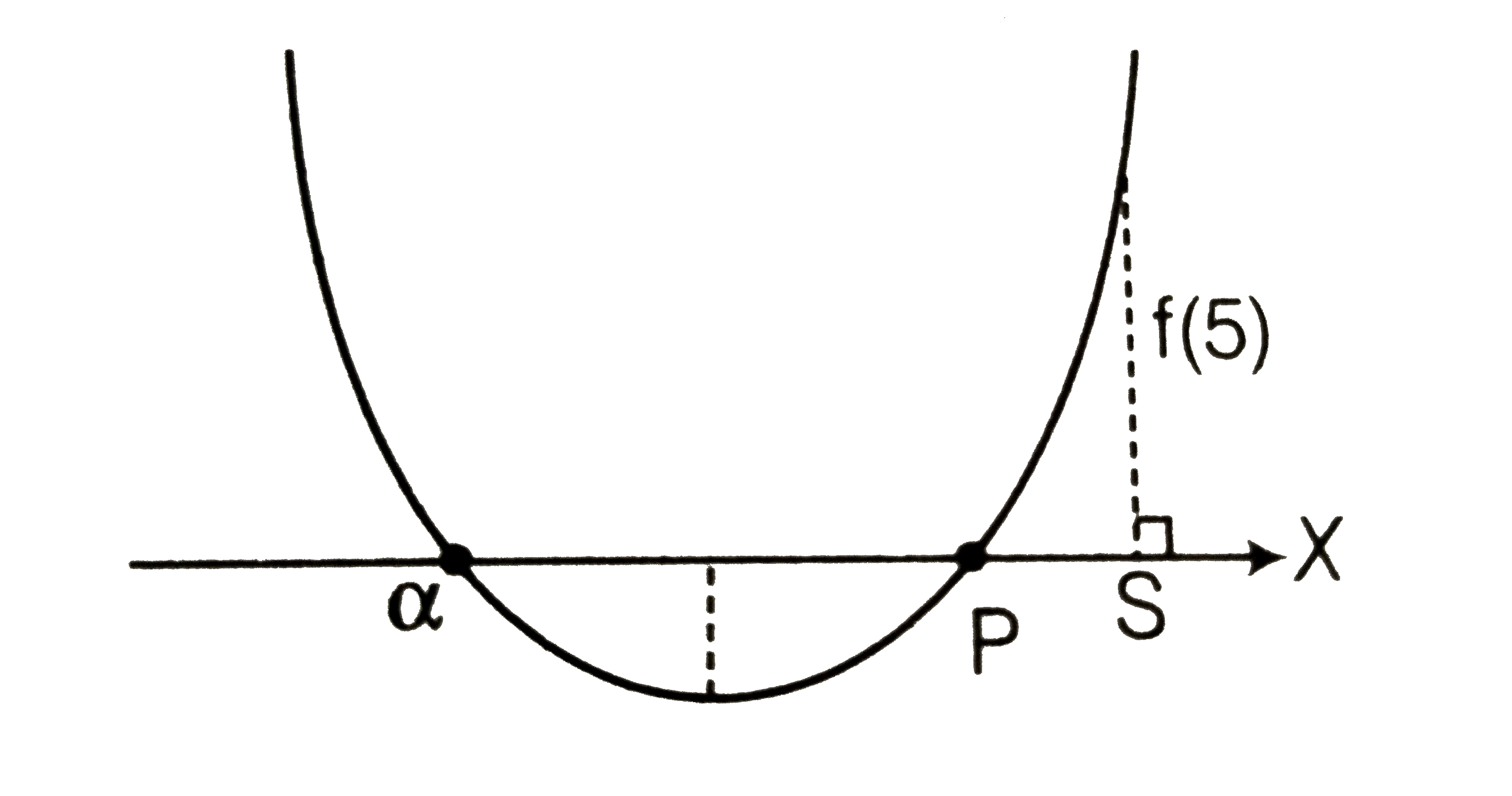
Case I D≥0
⇒4k2−4.1(ik2+k−5)≥0
⇒−4(k−5)≥0
⇒k−5≤0
⇒k≤5 or kε(−∞,5]
Case II x-Coordinate of vertex x<5
⇒2k2<5
⇒k<5 or kε(−∞,5)
Case III f(5)>0
⇒2−10k+k2+k−5>0
⇒k2−9k+20>0
⇒(k−4)(k−5)>0 or kε(−∞,4)∪(5,∞)
Combining all cases, we get
kε(−∞,4)
Similar Questions
If the quadratic equation x2+2(k+1)x+9k−5=0 has exactly one positive root, then k lies in the set
View Solutionयदि द्विघात समीकरण x2−2kx+k2+k−5=0 के दोनों मूल 5 से छोटे है, तो k किस अन्तराल में स्थित है -
View SolutionIf both the roots of the quadratic equation x2−2kx+k2+k−5=0 are less than 5, then k lies in the interval.
View SolutionIf both the roots of the quadratic equation x2−2kx+(k2+k−5)=0 are less than 5, then k lies in the interval
View SolutionIf one root is greater than 2 and the other root is less than 2 for the equation x2−(k+1)x+(k2+k−8)=0, then the value of k lies between
View SolutionIf both the roots of the quadratic equation x2−2kx+k2+k−5=0 are less than 5 , then k lies in the interval
View SolutionIf both the roots of the quadratic equation x2−2kx+k2+k−5=0 are less than 5, then k lies in the interval.
View SolutionIf both the roots of the equation x2−12kx+k2+k−5=0 are less than 5, then k lies in the inverval
View Solution
