If both the roots of the quadratic equation x2−2kx+k2+k−5=0 are less than 5, then k lies in the interval.Solution in Punjabi
(−∞,4)
[4,5]
(5,6)
(6,∞)
The correct Answer is:A
Let f(x)=x2−2kx+k2+k then α
Consider the following cases:
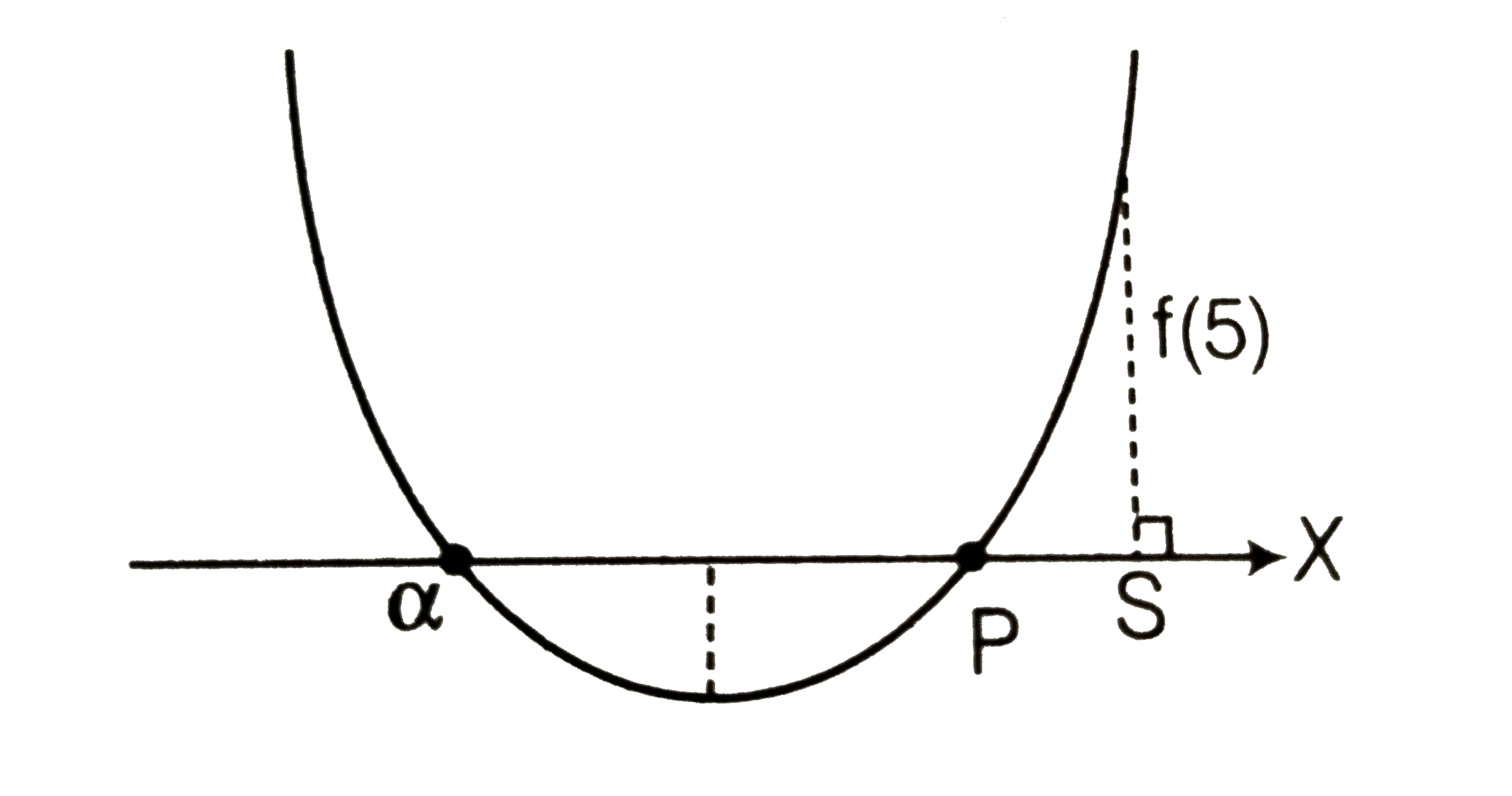
Case I D≥0
⇒4k2−4.1(ik2+k−5)≥0
⇒−4(k−5)≥0
⇒k−5≤0
⇒k≤5 or kε(−∞,5]
Case II x-Coordinate of vertex x<5
⇒2k2<5
⇒k<5 or kε(−∞,5)
Case III f(5)>0
⇒2−10k+k2+k−5>0
⇒k2−9k+20>0
⇒(k−4)(k−5)>0 or kε(−∞,4)∪(5,∞)
Combining all cases, we get
kε(−∞,4)
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Subjective Type Questions)24videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - The Straight Lines Exercise 8 : (Questions Asked in Previous 13 years Exams)1videos
THE STRAIGHT LINES
- BOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam2videos
THREE DIMENSIONAL COORDINATE SYSTEM
Similar Questions
For what values of m the equation (1+m)x2−2(1+3m)x+(1+8m)=0 has (m∈R)
(i) both roots are equal03:19View SolutionSolve the following system of inequalities graphically
x+5y≤25,2x+2y≥2,2x−2y≤0,x≥0,y≥004:46View SolutionConsider the line L1:x−12=y−1=z+31,L2:x−41=y+31=z+32 find the angle between them.
04:46View SolutionIf both roots of the quadratic equation x^(2)+x(4-2k)+k^(2)-3k-1=0 are less than 3, then k lies in the interval
09:10View Solutionयदि द्विघातीय समीकरण x2−2kx+k2+k−5=0 के दोनों मूल 5 से कम है तो k निम्न में इस कौन - से अंतराल में स्थित है ?
02:12View Solutionयदि द्विघात समीकरण x2−2kx+k2+k−5=0 के दोनों मूल 5 से छोटे है , तो k निम्न में से किस अन्तराल में स्थित है ?
04:58View SolutionIf one root of (k−5)x2−2kx+(k−4)=0 is less than 1 and the other root is greater than 2 then k in(a,b)then the value of a2−bis.
02:44View SolutionIf one root is greater than 2 and the other root is less than 2 for the equation x2−(k+1)x+(k2+k−8)=0, then the value of k lies between
02:15View SolutionIf the both the roots of the quadratic equation x2−2kx+k2+k−5=0 are less than 5, then k
03:16View SolutionFind the value of k so that the sum of the roots of the quadratic equation is equal to the product to the roots :
(k+1)x2+2kx+4=0View SolutionIf the roots of the quadratic equation x2−2kx+2k2−4=0 are real,then the range of the values of k is
07:18View SolutionIf the roots of x2−2kx+k2−1=0 lie between -2 and 4 then the interval in which k lies, is
02:47View SolutionIf the quadratic equation x2+2(k+1)x+9k−5=0 has exactly one positive root, then k lies in the set
02:10View Solutionयदि द्विघात समीकरण x2−2kx+k2+k−5=0 के दोनों मूल 5 से छोटे है, तो k किस अन्तराल में स्थित है -
02:44View Solutionk का मान ज्ञात कीजिए जिसमे द्विघात समीकरण (k+1)x2+2kx+4=0 के मूलों का योग मूलों की गुणा के समान हो।
02:57View SolutionFind the value of k by which the quadratic equation (k+1)x^(2)+2kx+4=0 The sum of the roots of is equal to the multiplication of the roots.
03:10View Solution
