Two chords AB and CD of a circle intersect each other at P internally. If AP = 3.5 cm, PC = 5 cm, and DP = 7 cm, then what is the measure of PB?
8 cm
12 cm
10 cm
10.5 cm
The correct Answer is:C
To solve the problem step by step, we can use the property of intersecting chords in a circle. The property states that if two chords intersect each other inside a circle, then the products of the lengths of the segments of each chord are equal.
1. Identify the Given Values:
- Let AP=3.5cm
- Let PC=5cm
- Let DP=7cm
- We need to find PB.
2. Apply the Intersecting Chords Theorem:
According to the theorem:
AP×PB=PC×PD
3. Substitute the Known Values:
Substitute the known lengths into the equation:
3.5×PB=5×7
4. Calculate the Right Side:
Calculate 5×7:
5×7=35
So the equation becomes:
3.5×PB=35
5. Solve for PB:
To find PB, divide both sides by 3.5:
PB=353.5
6. Simplify the Division:
To simplify 353.5, we can multiply the numerator and denominator by 10 to eliminate the decimal:
PB=35×103.5×10=35035=10
7. Final Answer:
Thus, the length of PB is:
PB=10cm
- Let AP=3.5cm
- Let PC=5cm
- Let DP=7cm
- We need to find PB.
According to the theorem:
AP×PB=PC×PD
Substitute the known lengths into the equation:
3.5×PB=5×7
Calculate 5×7:
5×7=35
So the equation becomes:
3.5×PB=35
To find PB, divide both sides by 3.5:
PB=353.5
To simplify 353.5, we can multiply the numerator and denominator by 10 to eliminate the decimal:
PB=35×103.5×10=35035=10
Thus, the length of PB is:
PB=10cm
Similar Questions
Two chords AB and CD of a circle intersect at a point P inside the circle. If AB = 7cm , PC = 2 cm and AP = 4 cm, then CD is equal to:
एक वृत्त की दो जीवाएं AB और CD वृत्त के भीतर बिंदु P पर एक दूसरे को काटती हैं | यदि AB = 7 सेमी, PC = 2 सेमी और AP = 4 सेमी है, तो CD किसके बराबर होगा ?
View SolutionIn the given figure, O is the centre of the circle. Its two chords AB and CD intersect each other at the point P within the circle. If AB = 18 cm, PB = 8 cm, CP = 5 cm, then find the length of CD.
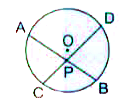
View Solution
Knowledge Check
Chords AB and CD of a circle intersect externally at P. If AB=6cm,CD=3cmandPD=5cm, then the length of PB is
A5 cmB7.35 cmC6 cmD4 cmChords AB and CD of a circle intersect at a point P inside the circle. If AB = 10 cm, AP = 4 cm and PC = 5 cm, then CD is equal to:
A4.8 cmB6.8 cmC9.8 cmD7.8 cmTwo chords AB and CD of a circle intersects each other at P. which of the following is correct?
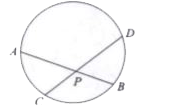 AAP×PB=CP×PDBAP+PB=CP×PDCAP−PB=CP−PDDAP×CP=BP×PD
AAP×PB=CP×PDBAP+PB=CP×PDCAP−PB=CP−PDDAP×CP=BP×PD
Chords AB and CD of a circle intersect at a point P inside the circle. If AB = 10 cm. AP = 4 cm and PC = 5 cm, then CD is equal to:
एक वृत्त की जीवायें AB और CD वृत्त के भीतर स्थित बिंदु P पर एक दूसरे को काटती हैं | यदि AB =10 सेमी,AP = 4 सेमी और PC = 5 सेमी है, तो CD का मान क्या होगा ?
View SolutionChords AB and CD of a circle intersect externally at P. If AB = 6 cm, CD = 3 cm and PB = 4 cm, then the length (in cm) of PD is :
एक वृत्त की जीवायें AB और CD एक दूसरे को बाहर से P पर काटती हैं | यदि AB = 6 सेमी,CD =3 सेमी और PB =4 सेमी है, तो PD की लंबाई (सेमी में ) ज्ञात करें |
View SolutionTwo chords AB, CD of a circle with centre O intersect each other at P. ∠ADP=23∘ and ∠APC=70∘, then the ∠BCDis
View SolutionTwo chords AB and CD of a circle are produced to intersect each other at point P outside the circle. If AB=7 cm, BP = 4.2 cm and PD = 2.8 cm, then the length of CD is: /
एक वृत्त की दो जीवाओं AB और CD को बढ़ाया जाता है जो एक-दूसरे को वृत्त के बाहर बिंदु ? पर काटती हैं| यदि AB = 7 सेमी, BP = 4.2 सेमी तथा तथा PD = 2.8 सेमी है, तो CD की लंबाई कितनी है ?
View SolutionThe two chords AB and CD of a circle intersect at point P, such that BP=4 cm, PD=5 cm, and CP=8 cm. find the length of chord AB.
View Solution