Question

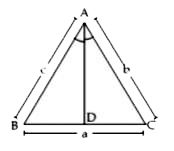
In triangle ABC, $AD\perp BC$ and AO is the bisector of $\angle BAC.$ If $\angle ABC={65}^{\circ }\text{and}\angle ACB=23\frac{1^{\circ }}{2}$ , then $\angle DAO$ is ____ (in degrees)

Options

A. `20(1^@)/4`
B. `20(1^@)/5`
C. `20(1^@)/2`
D. `20(3^@)/4`

Answer

D

Explanation

To solve the problem, we need to find the angle $$\angle DAO$$ in triangle $$ABC$$ where $$AD$$ is perpendicular to $$BC$$ and $$AO$$ is the angle bisector of $$\angle BAC$$. Given that $$\angle ABC={65}^{\circ }$$ and $$\angle ACB={23.5}^{\circ }$$, we can follow these steps:

Step 1: Find \( \angle BAC \)
We know that the sum of angles in a triangle is \( 180^\circ \). Therefore, we can express \( \angle BAC \) as follows:

\( \angle BAC = 180^\circ - \angle ABC - \angle ACB \)

Substituting the given values:

\( \angle BAC = 180^\circ - 65^\circ - 23.5^\circ \)

Calculating this gives:

\( \angle BAC = 180^\circ - 88.5^\circ = 91.5^\circ \)

Step 2: Find \( \angle BAO \) and \( \angle OAC \)
Since \( AO \) is the bisector of \( \angle BAC \), we can find \( \angle BAO \) and \( \angle OAC \) as follows:

\( \angle BAO = \angle OAC = \frac{1}{2} \angle BAC \)

Substituting the value of \( \angle BAC \):

\( \angle BAO = \angle OAC = \frac{1}{2} \times 91.5^\circ = 45.75^\circ \)

Step 3: Find \( \angle DAC \)
In triangle \( ACD \), we know that \( AD \) is perpendicular to \( BC \), which means \( \angle ADC = 90^\circ \). We can find \( \angle DAC \) using the fact that the angles in triangle \( ACD \) also sum to \( 180^\circ \):

\( \angle DAC + \angle ACD + \angle ADC = 180^\circ \)

Substituting the known values:

\( \angle DAC + 45.75^\circ + 90^\circ = 180^\circ \)

Calculating this gives:

\( \angle DAC + 135.75^\circ = 180^\circ \)

\( \angle DAC = 180^\circ - 135.75^\circ = 44.25^\circ \)

Step 4: Find \( \angle DAO \)
Since \( \angle DAO \) is equal to \( \angle BAO \), we have:

\( \angle DAO = \angle BAO = 45.75^\circ \)

Thus, the final answer is:

\( \angle DAO = 45.75^\circ \)