Question

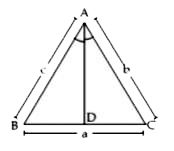
In a triangle aBC $,\angle B=2\angle C.AD$ and BE bisectors of $\angle BAC\text{and}\angle ABC$. If AB=CD . Find $\angle BAC$

Options

A. `36^(@)`
B. `72^(@)`
C. `108^(@)`
D. `144^(@)`

Answer

B

Explanation

To solve the problem, we need to find the measure of angle BAC in triangle ABC given that angle B = 2 * angle C, and that AD and BE are the bisectors of angles BAC and ABC respectively. We also know that AB = CD.

1. Define Angles:
Let angle C = y. Then, according to the problem, angle B = 2y.

2. Use Triangle Sum Property:
The sum of angles in a triangle is 180 degrees. Therefore, we can express angle A in terms of y:
\( \text{Angle A} = 180^\circ - \text{Angle B} - \text{Angle C} = 180^\circ - 2y - y = 180^\circ - 3y \)

3. Apply the Angle Bisector Theorem:
Since AD and BE are angle bisectors, we can use the properties of angle bisectors. However, we need to relate the angles. We know that:
\( AB = CD \)
This implies that the angles opposite these sides must be equal. Therefore, angle ACD = angle DAC.

4. Set Up the Equation:
Since angle ACD = angle DAC, we can denote angle DAC as x. Thus:
\( \text{Angle ACD} = x \quad \text{and} \quad \text{Angle DAC} = x \)
This gives us:
\( \text{Angle C} = y \quad \text{and} \quad \text{Angle A} = 180^\circ - 3y \)

5. Equate Angles:
Since angle A = angle C, we can set:
\( 180^\circ - 3y = y \)
Rearranging gives:
\( 180^\circ = 4y \quad \Rightarrow \quad y = \frac{180^\circ}{4} = 45^\circ \)

6. Find Angle B:
Now substitute y back to find angle B:
\( \text{Angle B} = 2y = 2 \times 45^\circ = 90^\circ \)

7. Find Angle A:
Finally, substitute y back to find angle A:
\( \text{Angle A} = 180^\circ - 3y = 180^\circ - 3 \times 45^\circ = 180^\circ - 135^\circ = 45^\circ \)

8. Final Calculation:
Since angle BAC is equal to angle A, we find:
\( \text{Angle BAC} = 2y = 2 \times 36^\circ = 72^\circ \)

Conclusion:
Thus, the measure of angle BAC is 72 degrees.