A narrow beam of singly charged potassium ions of kinetic energy 32keV is injected into a region of width 1.00 cm having a magnetic field of strength 0.500 T as shown in . The ions are collected at a screen 95.5cm away from the field region. If the beam contains isotopes of atomic weights 39 and 41, find the separation between the points where these isotopes strike the screen. Take the mass of a potassium ion=A(1.6X10−27) kg where A is the mass number.
 Solution in Tamil
Solution in Tamil
For E-39
m=39×1.6×10−7)kg,<br>B=5×10−1T,
q=1.6×10−10_(c),KE=32kev
Velocity projection
12×3sinθ×(1.6×10−27) ,
rArr V2=32×102×106×10−19
V=4.05×106
Through out the motion the horiantal velocity remation constant
i = 24 xx 10^(-18) sec <br>[timetaken→crossthemag≠ticfield]<br>A≤∈theregionhav∈gmag≠ticfield.<br> = 5193 , 53 xx 10 ^(4) m/s ^(2) <br>V(∈verticaldirection)=at<br> 5193.53 xx 10^(8) xx 24 xx 10^(-18) <br> = 12464.48 m/s <br>Totaltimetaken→reachthescreen<br> = 0.000002382 sec,<br>Timegap=2382×10−0−24×10−2sec ,
=2358×10−2sec
Distance moved vertically (in the time)
=12464.48×2358×10−0
= 0.0293m <br> v^(2) = 2aS<br>Netdisplayoml∈e<br> = 0.0001495 + 0.0293912<br> = 0.0295407 on<br>forK−41l:<br>12×41×1.6×10−17v2
=32×100×1.6×10−0 lt.brgt ⇒v=39.509ms
a=4818.193×100ms2
i = ( time taken for comming outside from magnetic field ltbbbrgt =25×10(−0)sec
V = at (vertical velocity )
=4818.193×108×25×10−0
=12045.48msltlbrgt ( time total to reach the screen )
=0.000002442
timegap=2442×10−0−25×10−8
=2417×10−8
distance moved vericaily
=12045.48×2417×10−0
=0.0291
Now V2=2aS=(2045.48)2
2×4818.19×106S
⇒S=0.0001505m
Net distance traveiled
=0.0001505+0.0291139
=0.0292644
Net gap between K−39andK−41
=0.0295407−0.0292644
0.0001763m=0.27mm .
Topper's Solved these Questions
Similar Questions
If a charged particle at rest experiences no electromagnetic force, then electric field in that region
03:59View SolutionFind the range of frequency of light that is visible to an average human being (400nm<λ<700nm)
02:20View SolutionUsing the formulae ((→F)=(→qv)×(→B)andB=(μ0)i2πr,find the SI units of the magnetic field B and the permeability constant
05:00View SolutionSingly charged magnesium (A=24) ions are accelerated to kinetic energy 2keV and are projected perpendicularly into a magnetic field B of magnitude 0.6 T. (a) Find the radius of the circle formed by the ions. (b) If there are also singly charged ions of the isotope magnesium.26, what would be the radius for these particles?
02:50View SolutionProtons having kinetic energy K emerge from an accelerator as a narrow beam. The beam is bent by a perpendicular magnetic field so that it just misses a plane target kept at a distance I in front of the accelerator. Find the magnetic field.
View SolutionA narrow beam of singley charged carbon ions, moving at a constant velocity of 6.0X104ms−1, is sent perpendicularly in a rectangular region having uniform magnetic field B=0.5 T . It is found that two beams emerge from the field in the backward derection, the separations from the incident beam being 3.0 cm and 3.5cm. Identify the isotopes persent in the ion beam. Take the mass of an ion = A(1.6X10−27 kg, where A is the mass number.
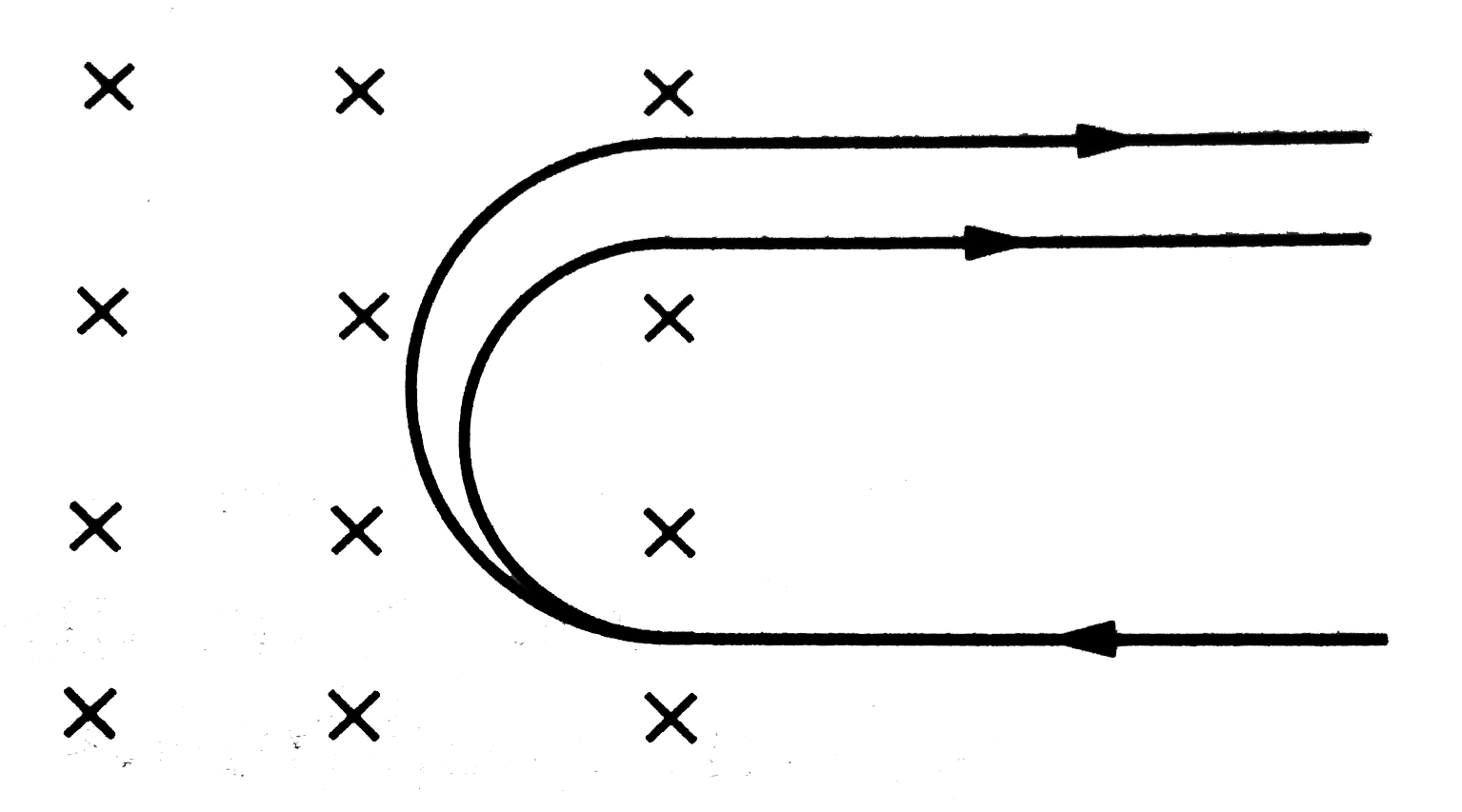 03:26View Solution
03:26View SolutionMixed He+ and O2+ ions (mass of He+=4 amu and that of O2+=16 amu) beam passes a region of constant perpendicular magnetic field. If kinetic energy of all the ions is same then
View SolutionA narrow beam of identical ions with specific charge q//m , possessing different velocities, enters the region of space, where there are unifrom parallel electric and marnetic fields the strength E and induction B , at the point O (see Fig). The beam direction coincides with the x axis at the point O . A plane screen oriented at right angles to the x axis is located at a distance l from the point O . Find the equation of the trace that the ions leave on the screen. Demonstrate that at x lt lt l it is the equaction of a parabola.
10:32View SolutionA long uniform cylindrical beam of radius R consists of positively charged particles each of charge q, mass m and velocity V along positive x direction. The axis of the beam is the x-axis. The beam is incident on a region having magnetic field in y-z plane. The magnetic field in the region is confined to 0lexleDeltax(Deltax "is small"). The field lines are circular in yz plane as shown. The magnitude of the field is given by B = B_(0) r where B_(0) is a constant and r is distance from the origin. Show that this magnetic field acts as a converging lens for the ion beam and obtain the expression for focal length. Neglect the divergence in the beam caused due to electromagnetic interaction of the charge particles.
View SolutionWhen electron beam passes through an electric field,they gain kinetic energy. If the same beam passes through magnetic field, then
02:34View SolutionA narrow beam of identical ions with specific charge q/m, possessing different velocities, enters the region of space, where there are uniform parallel electric and magnetic fields with strengths E and B , at the point O. The beam direction coincides with the x-axis at the point O. A plane screen oriented at right angles to the x-axis is located at a distance I from O. Find the equation of trace that the ion leaves on the screen. Demonostrate that at z lt lt l , it is the equation of a parabola.
03:56View SolutionAn electron beam accelerated by a p.d. of V=100V enters into a magnetic field perpendicular out the plane of the page. The space occupied by the field is width d=10cm. A screen is held at right angles to the initial direction of motion of the beam at a distance b=20 cm from the nearer edge of the field. find the distance 'δ' of the point where the beam strikes the screen from the point where it whould strike had there been no field.
03:40View SolutionA thin beam of charged particles in incident normally on the boundry of a region containing a uniform magnetic field as shown.The beam comprise of mono energetic α and β(−) particles, each possessing a kinetic energy T.Neglecting interaction between particles of the beam, find the separation between the points on line PQ where the α and β particles emerge out of the magnetic field.(express your answer in terms of T,B,α(2e,mα)&β−(−e,me),where all terms have their usual meanings.)
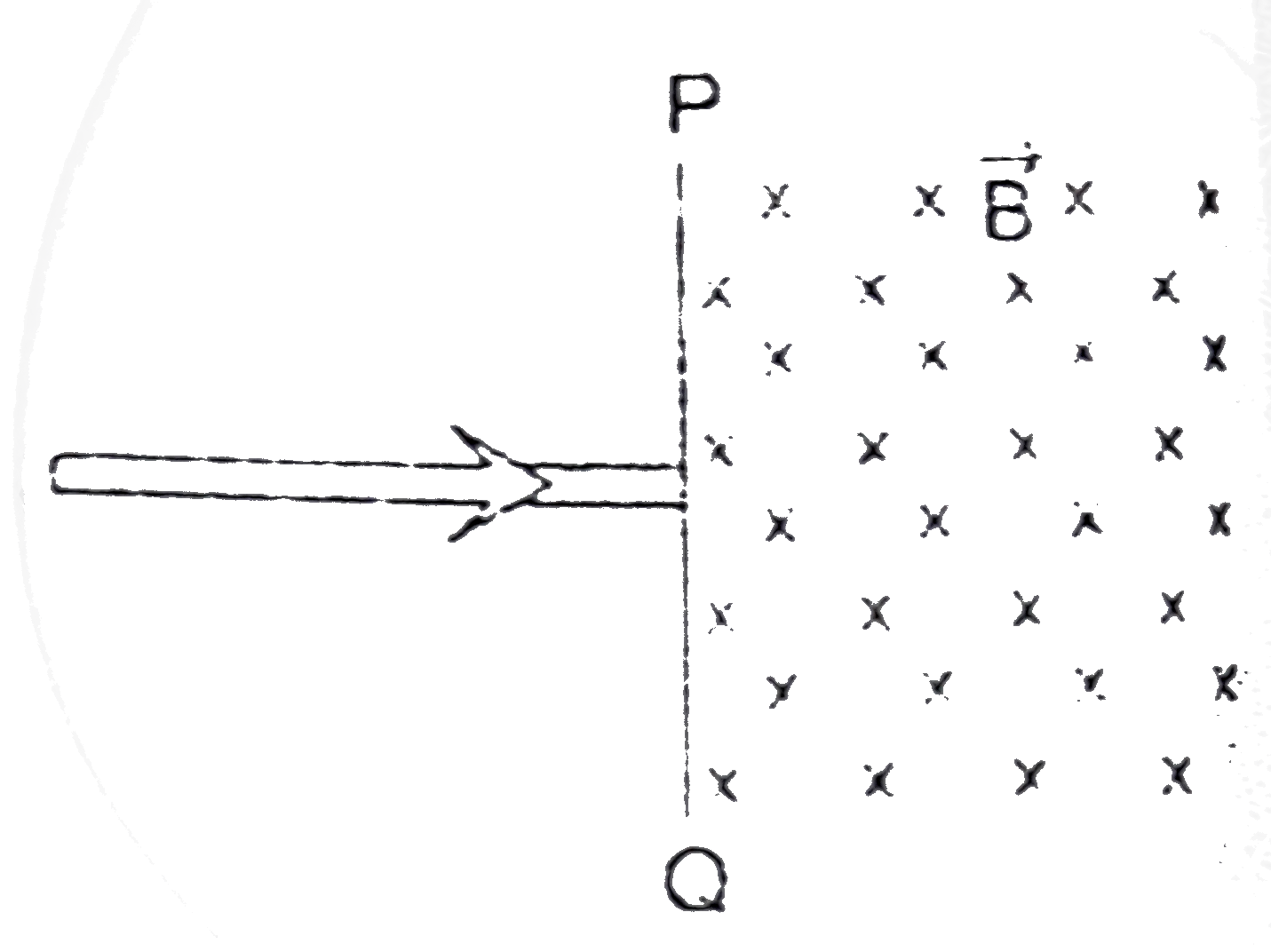 05:00View Solution
05:00View SolutionA cylindrical region of magnetic field is produced by an electromagnet as shown in the figure. A wint carrying a current of0.5 A is placed perpendicularly to the axis of the cylindrical region. If the magnetic field produced by the electromagnets is 2.0 T in strength and the radius of cylindrical region is 5 cm, find the magnetic force acting on the wire due to the magnetic field in the region.
 07:22View Solution
07:22View SolutionSingly charged magnesium (A=24) ions are accelerated to kinetic energy 2keV and are projected perpendicularly into a magnetic field B of magnitude 0.6 T. (a) Find the radius of the circle formed by the ions. (b) If there are also singly charged ions of the isotope magnesium.26, what would be the radius for these particles?
02:28View SolutionProtons having kinetic energy K emerge from an accelerator as a narrow beam. The beam is bent by a perpendicular magnetic field so that it just misses a plane target kept at a distance I in front of the accelerator. Find the magnetic field.
04:08View Solution
