A hemispherical portion of the surface of a solid glass sphere (mu = 1.5) of radius r is silvered to make the inner side reflecting. An object is placed on the axis of the hemisphere at a distance 3r from the centre of the sphere. The light from the object is refracted at the unsilvered part, then reflected from the silvered part and again refracted at the unsilvered part. Locate the final image formed. Solution in Tamil
The correct Answer is:A, C

For refracting surface μ1=1,u=−2r
μ2=32
v=?R=r
μ2v−μ1u=μ2−μ1R
3/(2r)+1/(2r)0.5/r<br>3/(2r)=1/(2r)rarr v=oo<br>nowforref≤ct∈gsurfaceu=−∞
f=r2,v=?
1v+1u=1f
1v=1∞=2r
→v=r2
from reflecting surface for reflecting surface
=u=−(2r−r2)=−3r2
μ=?,μ1=32
μ2=1
soμ2v−μ1u=μ2−μ1r
1v+3x22×3r=−0.5−r
1v=12r−1r=12r
so fiN/Al image will be at reflecting surface of sphere.
Topper's Solved these Questions
Similar Questions
If the light moving in a straight line bends by a small but fixed angle it may be a case of
View SolutionThe electric field in a region is given by →E=35E0→i+45E0→j with E0=2.0×103NC−1. Find the flux of this field through a recatngular surface of area 0.2m2 parallel to the y-z plane.
View SolutionFind the range of frequency of light that is visible to an average human being (400nm<λ<700nm)
View SolutionA point object is placed at the centre of a glass sphere of radius 6cm and refractive index 1.5. The distance of virtual image from the surface is
View SolutionA solid glass sphere with radius R and an index of refraction 1.5 is silvered over one hemisphere. A small object is located on the axis of the sphere at a distance 2R to the left of the vertex of the unsilvered hemisphere. Find the position of final image after all refractions and reflection have taken place.
View SolutionA point object is placed at the center of a glass sphere of radius 6cm and refractive index 1.5. The distance of virtual image from the surface is
View SolutionHalf the surface of a transparent sphere of refractive index 2 is silvered. A narrow, paralel beam of light is incident on the unsilvered surface, symmetrically with respect to the silvered part. The light finally emerging from theh sphere will be a
View Solutionएक बिन्दु-वस्तु 6 सेमी त्रिज्या तथा 1.5 अपवर्तनांक वाले काँच के ठोस गोले के केंद्र पर स्थित है | गोले कि पृष्ठ से इसके आभासी प्रतिबिम्ब की दूरी है :
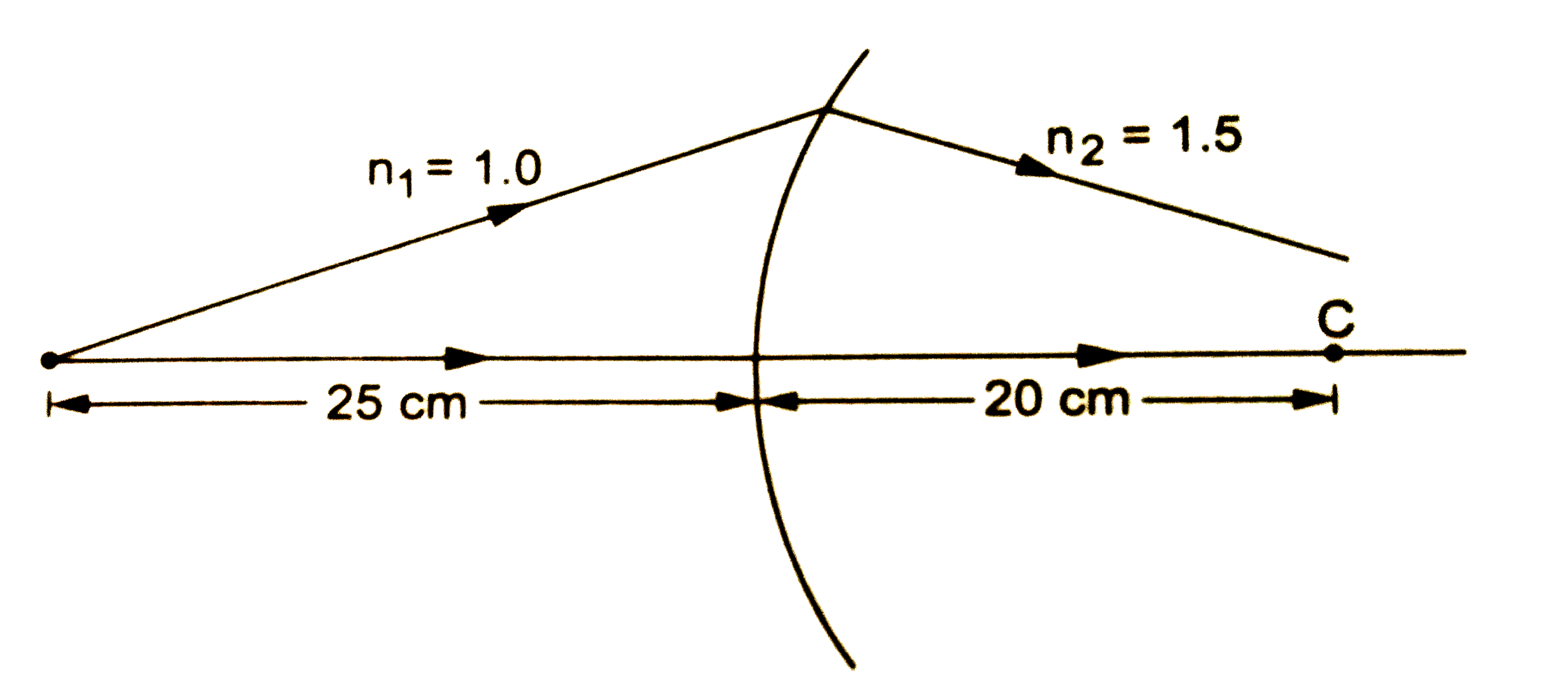
View Solutionचित्र में 1.5 अपवर्तनांक वाले कॉच के काँच के गोले का एक हिस्सा हवा में रखा हुआ दिखाया गया हैं । गोले की त्रिज्या 20 cm हैं । एक बिंदुस्त्रोत गोले की सतह से 25 cm दूर हवा में रखा हैं । अपवर्तन के कारण बने प्रतिबिंब का स्थान निर्धारित करें ।
View Solutionकाँच ( n = 1.5 ) के बने एक अर्ध्दगोलाकार ठोस की वक्र सतह को बाहर से सिल्वर कर इस सतह को परावर्तक बना दिया गया हैं । इसके अक्ष पर , केंद्र से 3r दूरी पर एक बिंदुस्त्रोत रखा गया हैं । इससे चला प्रकाश ठोस की समतल सतह से अपवर्तन , गोलीय सतह से परावर्तन तक समतल सतह से पुनः अपवर्तन के बाद पुनः हवा में निकल जाता हैं । स्त्रोत के अंतिम प्रतिबिंब का स्थान ज्ञात करें ।
View Solutionकाँच के एक गोले की वक्रता त्रिज्या 20 सेमी है। वायु में स्थित वस्तु का प्रतिबिंब गोले (μ=1.5) के अदंर इस प्रकार बनता है कि गोले के पृष्ठ से वस्तु और उसके प्रतिबिंब की दूरी समान रहती है, गोले के पृष्ठ से वस्तु की दूरी ज्ञात कीजिए।
View SolutionThere is a point object at the center of a glass sphere of diameter 12cm and refractive index 1.5 . The distance of the virtual from the surface of the sphere is
View SolutionThere is a point object at the centre of a glass sphere of diameter 12 cm and refractive index 1.5 . Calculate the distance (in cm) of the image from the surface of the sphere.
View SolutionA point object is placed at the centre of a glass sphere of radius 6 cm and μ=1.5. The distance of virtual image from the surface of sphere is :
View SolutionHalf the surface of a transparent sphere of refractive index 2 is silvered. A narrow, parallel beam of light is incident on the unsilvered surface, symmetrically with respect to the silvered part. The light finally emerging from the sphere will be a
View SolutionA point object is placed at the centre of a glass sphere of radius 6 cm and refractive index 1.5. The distance of the virtual image from the surface of the glass is
View Solution
