Consider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d
 Solution in Tamil
Solution in Tamil
The correct Answer is:A, B, C, D
i. when z=Dλ2d,atS4
minimum intensilty occurs, (dark fringe)
→Amplitude=0
At S3 path differenc e=0<br>→maxiμm∫ensityours.<br>→Amplitude=2r<br>SoonSigma^2screen,<br>l_(max)/l_(min)=((2r+0)^2)/((2r-0)^2)=1<br>ii.Whenz=λDd
As S4 maximum intensity occurs
→Amplitude=√2r
At S3 also maximum intensity occurs.
lmaxlmin=(2r+2r)2(2r−2r)2=∞
iii When z=λD4d,atS4
intensity =l_(max)/2<br>rarr Amplitude=sqrt2r<br>:. At S_3Intensi<yisminiμm<br>rarr Amplitude =2r
lmaxlmin=(2r+√2r)2(2r−√2r)2=34
Topper's Solved these Questions
Similar Questions
A light wave can travel
View SolutionA concave mirror having a radius of curvature 40 cm is placed in front of an illuminated point source at a distance of 30 cm from it. Find the location of the image.
View SolutionAn alpha particle is projected vertically upward a speed of 3.0X104kms−1 in a region where a magnetic field of magnitude 1.0 T exists in the direction south to north. Find the magnetic force that acts on the a particle.
View SolutionIn a Young's double slit interference experiment the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength λ. Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one fourth of the maximum.
View SolutionConsider the situation shown in fig. The two slits S_(1) and S_(2) placed symmetrically around the central line are illuminated by monochromatic light of wavelength lambda . The separation between the slit is d. The ligth transmitted by the slits falls on a screen S_(0) placed at a distance D form the slits. The slit S_(3) is at the central line and the slit S_(4) is at a distance z from S_(3) Another screen S_(c) is placed a further distance D away from S_(c) Find the ratio of the maximum to minimum intensity observed on S_(c) If z = (lambda D)/(2 d)
View SolutionConsider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
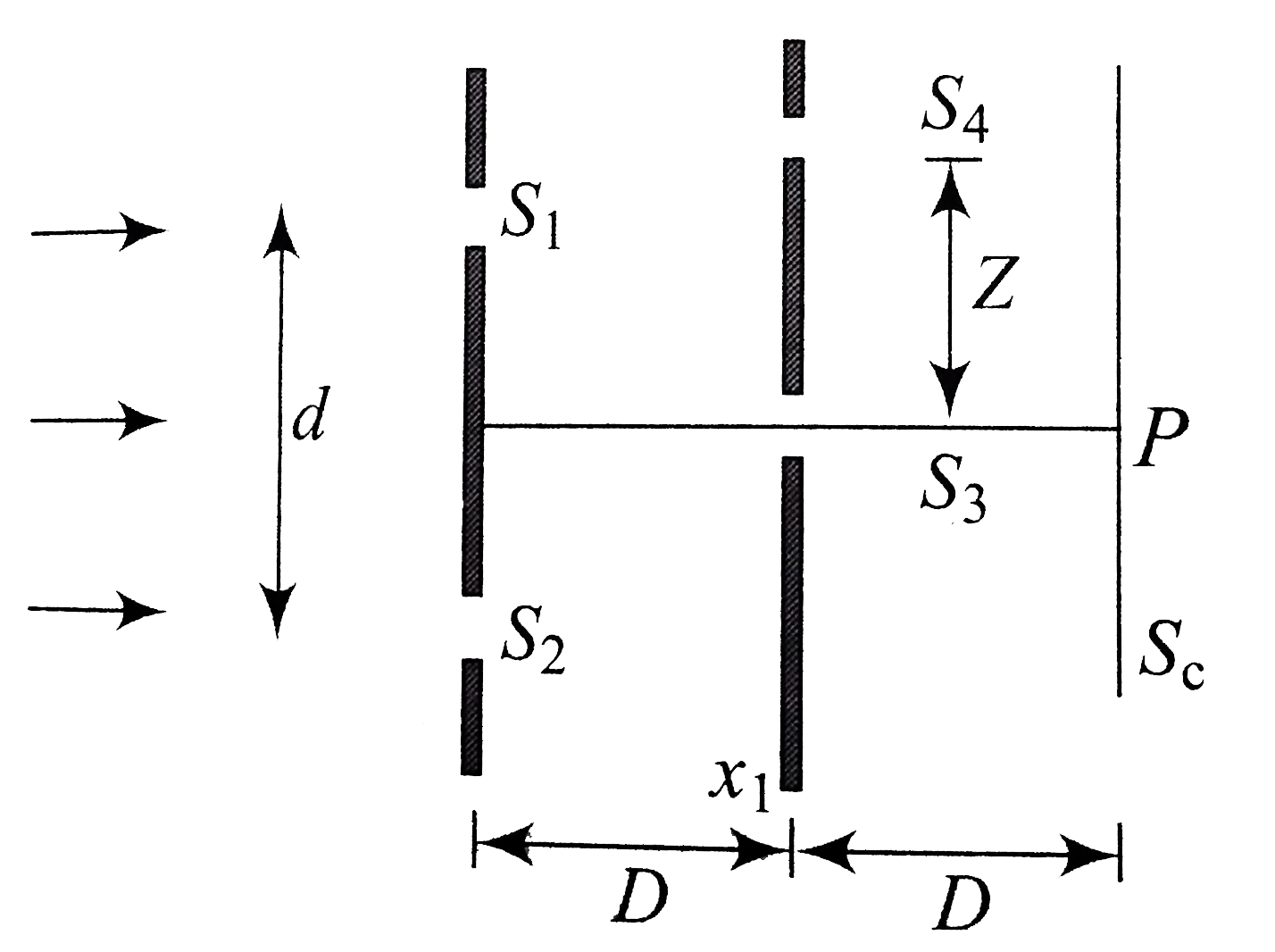
If z=λDd
View SolutionConsider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
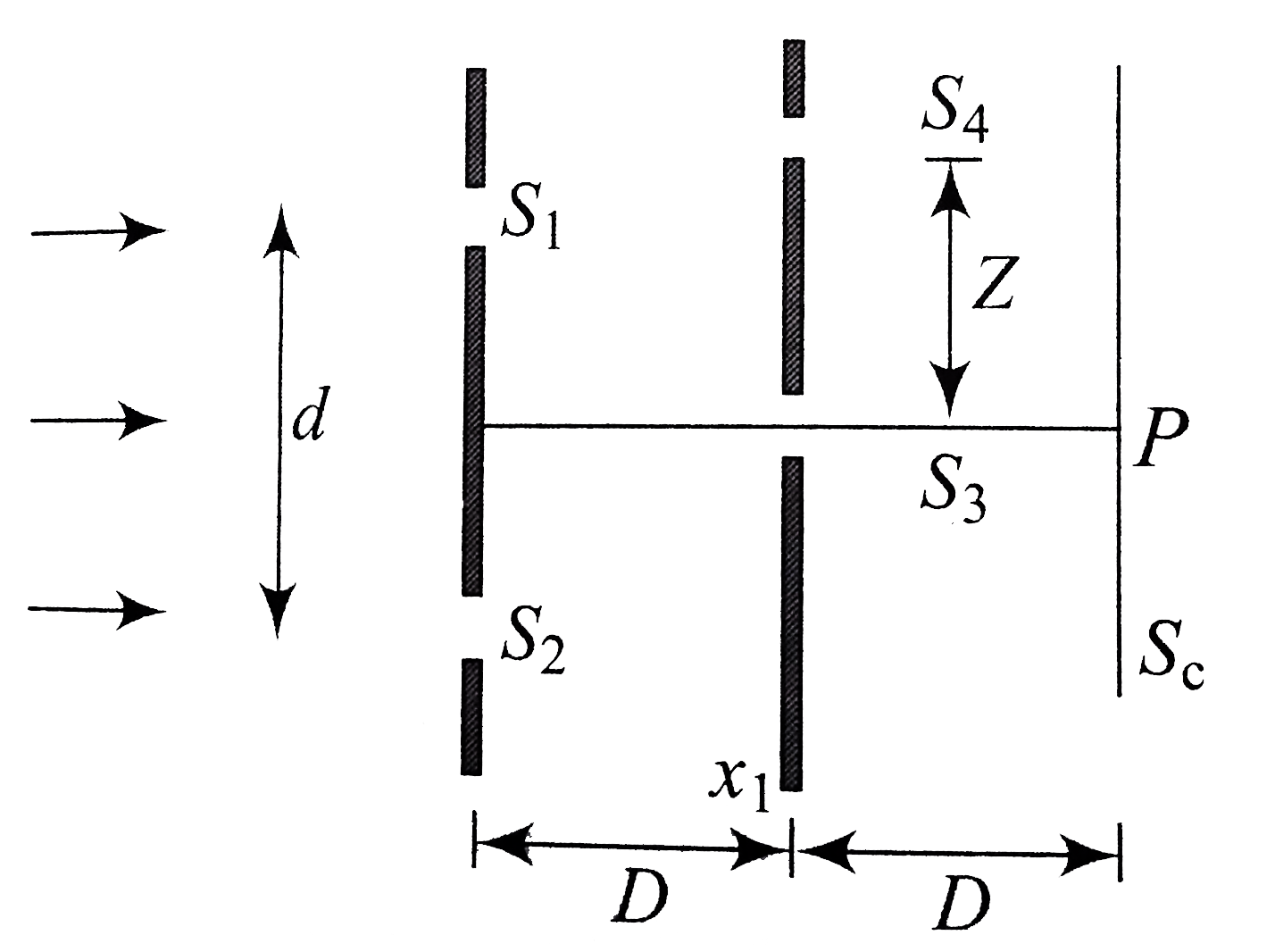
If z=λD4d
View SolutionIn a double slit experiment, the separation between the slits is d and distance of the screen from slits is D. If the wavelength of light used is lambda and I is theintensity of central bright fringe, then intensity at distance from central maximum is
View SolutionConsider the situation shown in figure-6.35. The two slits S1 and S2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen E1 placed at a distance D from the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3. Another screen E2 is placed a further distance D away from E1. Find the ratio of the maximum to minimum intensity observed on E2 if z is equal is : (a)λD2d (b)λDd (c)λD4d

View SolutionMonochromatic light from a narrow slit illuminates two parallel slits producing an interference pattern on a screen. The separation between the two slits is now doubled and the distance between the screen and the slits is reduced to half. The fringe width
View SolutionIn a double slit experiment, the separation between the slits is d and distance of the screen from slits is D. If the wavelength of light used is λ and I is the intensity of central bright fringe, then intensity at distance from central maximum is
View SolutionA light of wavelength λ falls on a narrow slit of width d.A diffraction fringe is formed on a screen placed at distance D from the slit. If the linear width of the central maximum equals to the width of the slit, will be the value of D?
View SolutionIn a Young's double slit interference experiment the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength λ. Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one fourth of the maximum.
View SolutionIn a Young's double slit interference experiment the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength λ. Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one fourth of the maximum.
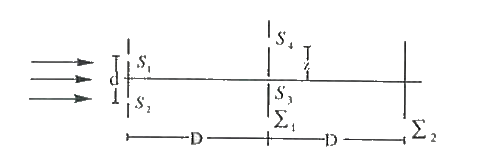
View SolutionConsider the situation shown in figure , The two slits S1andS2 placed symmetrically around the central line are illumated by a monocharmotic by a monocharomatic light of wavelength λ . The separation between the slits is d . The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits . The slit S3 is at the central line and the slit S4 is at a distance z from S3 .Another screen Σ2 is placed a further distance D away from Σ1 .Find the ratio of the minimum intensity observed on Σ2 if z is equal to
(1) z=λD2d
(2) λDd
(3) λD4d
View SolutionIn a Young's double slit interference experiment the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength λ. Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one fourth of the maximum.
View Solution

