Consider the arrangement shownin figure. By some mechanism,the separation between the slits can be changed. The intensity in measured at the point P which is at the common perpendicular bisector of z=(Dlamda)/(2d)
 Solution in Tamil
Solution in Tamil
The correct Answer is:A, B, C
a. When
So,
S_3 and S_4rarr At S_3S_3=0rarrl_1=0S_4 Intensity at S_4=0rarr
rarr Phase difference =0rarr l=l_1+l_2+2sqrt(l_1l_2)costheta^@=0+0+0=0rarr intensilty at P=0
Topper's Solved these Questions
Similar Questions
A light wave can travel
View SolutionA concave mirror having a radius of curvature 40 cm is placed in front of an illuminated point source at a distance of 30 cm from it. Find the location of the image.
View SolutionAn alpha particle is projected vertically upward a speed of 3.0X104kms−1 in a region where a magnetic field of magnitude 1.0 T exists in the direction south to north. Find the magnetic force that acts on the a particle.
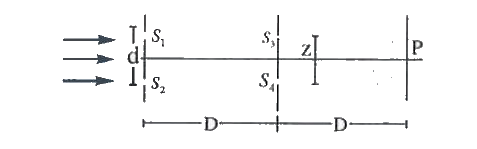
View SolutionConsider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d

View SolutionIn Young's double-slit experiment d/D=10−4 (d = distance between slits, D = distance of screen from the slits) At point P on the screen, resulting intensity is equal to the intensity due to the individual slit I0. Then, the distance of point P from the central maximum is (λ=6000Å)
View SolutionIn the arrangement shown in Fig., slits S1 and S4are having a variable separation Z. Point O on the screen is at the common perpendicular bisector of S1S2 and S3S4.
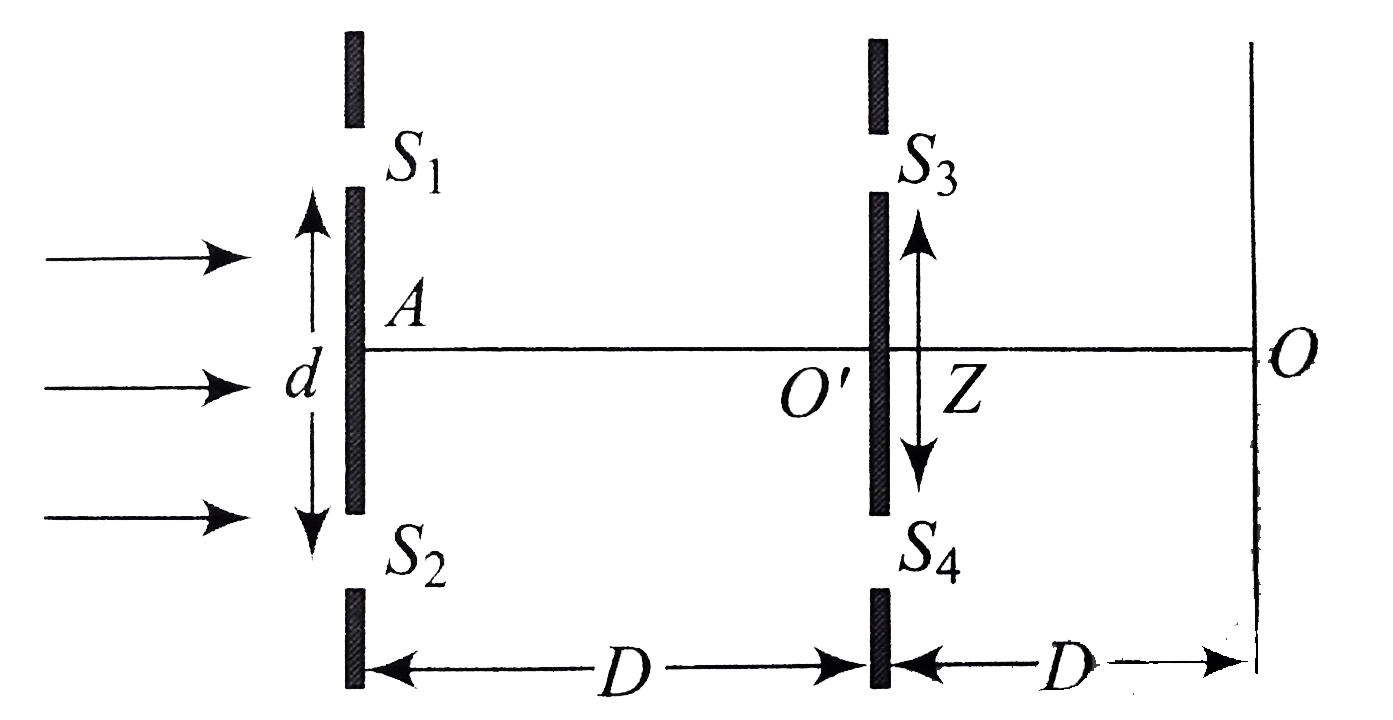
When Z=λD2d, the intensity measured at O is I0. The intensity at O When Z=2λDd is
View SolutionParallel monochromatic beam is falling normally on two slits S_(1) and S_(2) separated by d as shown in figure. By some mechanism, the separation between the slits S_(3) and S_(4) can be changed. The intensity is measured at the point P which is at the common perpendicular bisector of S_(1)S_(2) and S_(3)S_(4) . When z=(Dlambda)/(2d) , the intensity measured at P is I. and when z is equal to (4Dlambda)/(d) , Intensity is x l. Find x.
View SolutionIn Young's double-slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is lambda and d is the distance between the slits, the angular separation between point P and the center of the screen is
View SolutionIn Young's double slit experiment (d)/(D) = 10^(-4) (d = distance between slits, D = distance of screen from the slits) At a point P on the screen the resulting intensity is equal to the intensity due to individual slit I_(0) .Then the distance of point P from the central maximum is (lambda = 6000 Å) :
View SolutionIn a Young's double-slit interference pattern, the intensity of the central fringe at P=I0. When one slit width is reduced to half, the intensity at P will be
View SolutionIn the Young's doubel slit experiment, a poiint P on the central bright fringe is such that intensity of point P is 1/4 times the maximum intensity, distance between the slits is d and wavelength λ. Then angular separation of point P is
View Solutionयंग के द्विस्लिट प्रयोग में dD=10−4 (d = स्लिटों के बीच की दूरी, D = स्लिटों से पर्दे की दूरी ) पर्दे के बिन्दु P पुर परिणामी तीव्रता, एक स्लिट के कारण तीव्रता I0 के बराबर है। तब केन्द्रीय उच्चि्ठ से बिन्दु P की दूरी है (λ=6000Å)
View SolutionIn Young's double slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is λ and d is the distance between the slits, the angular separation between point P and the centre of the screen is ......
View SolutionConsider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d

View SolutionConsider the arrangement shown in figure. By some mechanism , the separation between the slits S3 slitS4can be changed . The intensity is measured at the point P which is at the common perpendicular between of S1,S2 When z=Dλ2d the intensity measured at P is l . Find the intensity when a is equal to 1 Dλd
2 . 3dλ2d
(3) 2Dλd
View SolutionYDSE में पर्दे की दूरी तथा दो स्लिटों के बीच दूरी क्रमशः D तथा 'd' है। केन्द्रीय उच्चिष्ठ से सबसे नजदीक वह बिन्दु, जिस पर तीव्रता केवल एक स्लिट से उत्पन्न तीव्रता के बराबर हो, की दूरी क्या होगी?
View Solution

