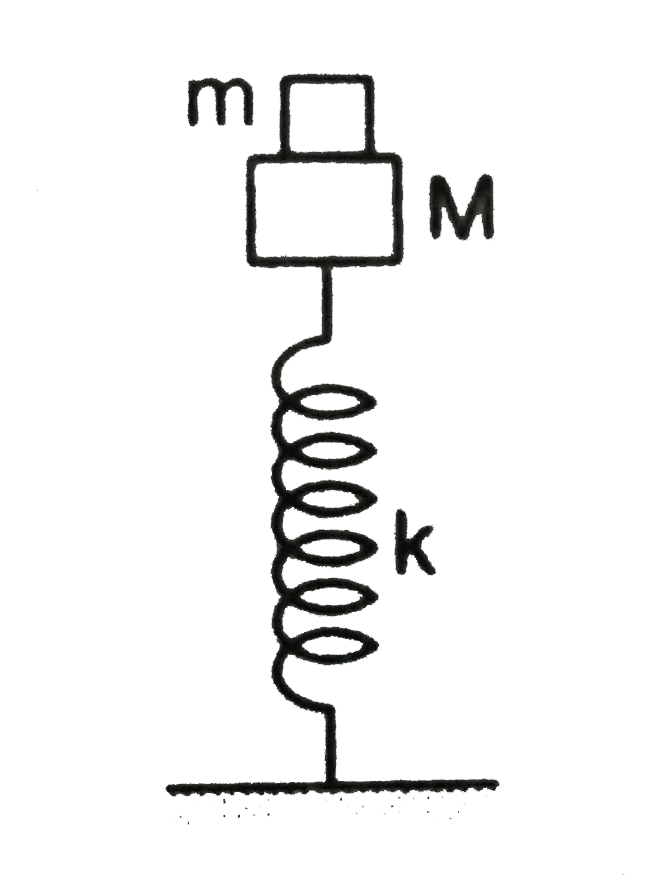
A small block of mass m is kept on a bigger block of mass M which is attached to a vertical spring of spring constant k as shown in the figure. The system oscilates verticaly. a.Find the resultant force on the smaller block when it is displaced through a distance x above its equilibrium position. b. find the normal force on the smaller blok at this position. When is this force smallest smaller block at this position. When is this force smallest in magnitude? c. What can be the maximum amplitude with which the two blocks may oscillate together?
 Solution in Tamil
Solution in Tamil
The correct Answer is:x=mkxM+m=<br≻mg−mkxM+N
maximum amplitude
=g(M+m)k
a. From the fre bdoy diagram
:. R+mωy2x−mg=0 ……….
Resultant force mω2x=mg−R
→mω2x=m(kM+m)x
x=mkxM+m
ω=√{kM+m}
[for spring mas system]
b. R=mg−mω2x
=mg−mmkM+Nx
=−mg−mkxM+N
For LR to be smallest mω2x should be max, i.e. x is maximum.
The particle should be at the highest point.
c. We have R=mg−mω2x
The two blocks may oscillate together in such a way that R is greater than 0.
At limiting condition R=0
mg=mω2x
=x=mgmω2=mg.(M+m)mk
So the maximum amplitude
=g(M+m)k
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
16 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
Select the correct statements
View SolutionA wheel is making revolutions about its axis with uniform angular acceleration. Starting from rest, till it reaches 100 rev/sec in 4 seconds. Find the angular acceleration.
View SolutionA load of 10 kg is suspended by a metal wire 3 m long and having a cross sectional area 4mm2. Find a. the stress b. the strain and c. the elongation. Young modulus of the metal is2.0×1011Nm−2
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionThe spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find

(a) the amplitude and the time period of the motion of the block,
(b) the energy stored in the spring when the block passes through the equilibrium position and
(c) the kinetic energy of the block at this position.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force.
View SolutionA block of mass m is attached to two unstretched springs of spring constant k , each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will be
View SolutionTwo springs are in a series combination and are attached to a block of mass 'm' which is in equilibrium. The spring constants and extension in the springs are as shown in the figure. Then the force exerted by the spring on the block is :

View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is

View SolutionTow identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrum position by a distance x towards right, find the restoring force.

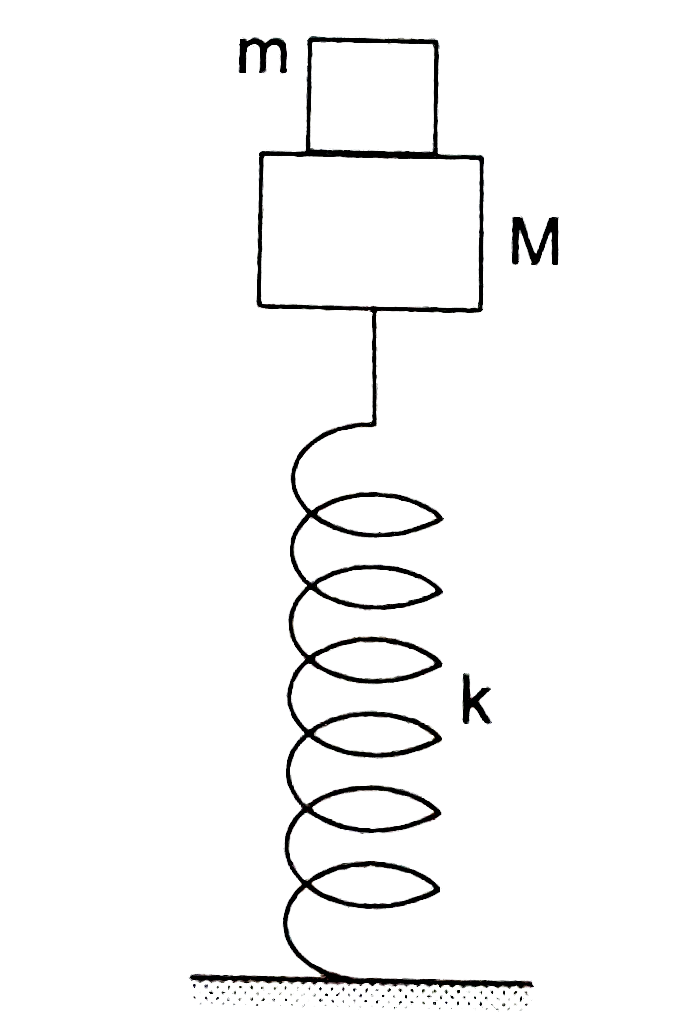
View Solutionएक स्प्रिंग को ऊर्ध्वाधर स्थिति में एक फर्श पर जड़कर रखा गया है (चित्र 21.E1) तथा इसपर M द्रव्यमान का एक ब्लॉक जड़ा हुआ है। इस ब्लॉक पर द्रव्यमान का एक दूसरा ब्लॉक रखा हुआ है। स्प्रिग के स्प्रिंग-नियताक k है। यह निकाय ऊर्ध्वाधर दोलन करता है। (a) जब ब्लॉक अपनी साम्यावस्था से x दूरी ऊपर है उस समय ऊपर बाले ब्लॉक पर परिणामी बल निकालें। (b) इस स्थिति में ऊपर वाले ब्लॉक पर नीचे बाले ब्लॉक द्वारा लगाया गया लबवत बल निकाले। इस लबवत बल का परिमाण किस स्थिति में न्यूनतम हगा? (c) दानो ब्लाकों को साथ-साथ दोलन करते रहने के लिए अधिकतम आयाम कितना हो सकता है
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force.

View SolutionTow identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrum position by a distance x towards right, find the restoring force.

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionThe spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find

(a) the amplitude and the time period of the motion of the block,
(b) the energy stored in the spring when the block passes through the equilibrium position and
(c) the kinetic energy of the block at this position.
View SolutionThe spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find the energy stored in the spring when the block passes through the equilibrium position .

View Solution
